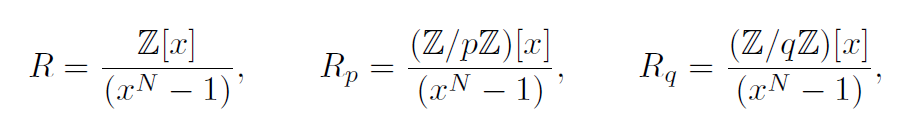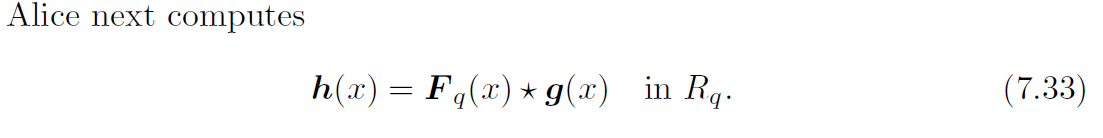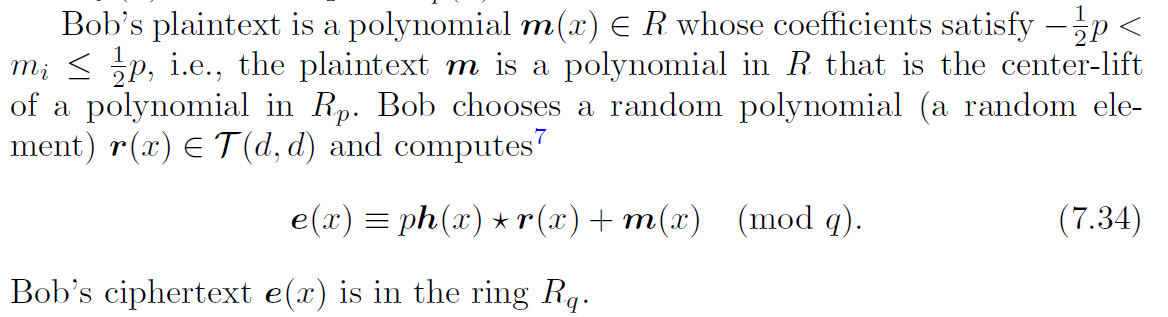NTRU学习笔记

NTRU是目前据我所知的最快的抗量子加密算法（当然NTRU也有也有签名算法）。

关于算法的Introduction我就不多说了，如果你之前了解过NTRU，那么我写的不一定会比你所了解的多；如果没了解过，可以先去谷歌或维基了解一下，也可以参考其官网上的文章。

NTRU到目前为止已经有很多版本，我参考的是[HPS14] 7.10 节的教科书版本，顺带一题，作者也是提出NTRU的三人（https://ntru.org/f/hps96.pdf）

参考：

[HPS14] Hoffstein J, Pipher J, Silverman J H, et al. An introduction to mathematical cryptography[M]. New York: springer, 2008.

PS：第一版好像是08年的，但我参考的是14年的第二版。

[HPS17] Hoffstein J, Pipher J, Schanck J M, et al. Choosing parameters for NTRUEncrypt[C]//Topics in Cryptology–CT-RSA 2017: The Cryptographers’ Track at the RSA Conference 2017, San Francisco, CA, USA, February 14–17, 2017, Proceedings. Springer International Publishing, 2017: 3-18.

PS：这篇主要讲的是参数设置。

要看懂下面的内容你可能需要：

• 数论知识（特别群论、环论）；
• 线性代数知识，多项式运算等；
• 基础的密码学知识（起码你得知道加密算法是干什么的吧）；
• Sagemath代码的读写经验；
• 足够的耐心。

理论知识·

多项式环和参数选取·

首先[HPS14]的7.10.1节一开始就扔出了三个卷积多项式环（Convolution Polynomial Rings），$R$、$R_p$和$R_q$，理解这三个环其实是理解NTRU的关键，接下来细说。

首先看$R$，分子（姑且先叫分子吧）的$\mathbb{Z}[x]$指的是整数域上的多项式，以符号$x$作为多项式的未知数，实际上也就是小学/初中开始接触的多项，比如$x^2+x+1$、$-2x^3-x$等。

然后，横线其实不是指除法，比起除法其实更像一个取余，或者叫商环（Quotient Ring，可以参考[HPS14]的2.10），大概意思是，“分子”上的多项式模上$x^N-1$后就会落在$R$上，其中N是NTRU的参数。其实跟RSA在$\mathbb{Z}_n^*$中运算所以要模$n$类似，可以做个类比方便理解。

举个栗子，假设取$N=2$，那就是$R = \frac{\mathbb{Z}[x]}{x^2-1}$，现在尝试把$\mathbb{Z}[x]$上的$x^2+x+1$转换到$R$上，由于“模数”是$x^2-1$，所以有

$$\begin{aligned} x^2-1 &\equiv 0 \ (\text{in } R) \end{aligned}$$

把这个关系利用到$x^2+x+1$上可以得到：

$$\begin{aligned} x^2+x+1 &\equiv x^2+x+1 - 0 \\ &\equiv x^2+x+1 - (x^2-1) \\ &\equiv x + 2 \ (\text{in } R) \end{aligned}$$

$x+2$就是最终落在$R$上的结果。

另一个栗子，$-2x^3-x$，这里偷一下懒，对其作分解后可以得到：

$$-2x^3-x = -2(x^2-1)·x - 3x$$

所以有：

$$\begin{aligned} -2x^3-x &\equiv -2(x^2-1)·x - 3x \\ &\equiv -2·0 - 3x \\ &\equiv -3x \ (\text{in } R) \end{aligned}$$

一般来说$R$中的多项式最高项不会大于等于$N$次，因为$x^N \equiv 1 \ (\text{in } R)$，所以每出现$x^N$都可以用$1$代替，可以利用这个方法检验最终结果的正确性（虽然我都是直接用Sage算的，逃）。

$R_p$其实类似，只不过其“分子”$(\mathbb{Z}/p\mathbb{Z})[x]$是系数模$p$的多项式，也就是多项式的系数需要进行模$p$操作，使其落在$\mathbb{Z}_p$中（$\mathbb{Z}/p\mathbb{Z}$其实就是$\mathbb{Z}_p$的另一种写法）。

举个栗子，设$p=3$，下面尝试把$-2x^3-x$转换到$(\mathbb{Z}/p\mathbb{Z})[x]$中：

$$\begin{aligned} -2x^3-x &\equiv (-2 \pmod p)x^3 + (-1 \pmod p)x \\ &\equiv (-2 \pmod 3)x^3 + (-1 \pmod 3)x \\ &\equiv x^3 + 2x \ (\text{in } (\mathbb{Z}/p\mathbb{Z})[x]) \end{aligned}$$

其实只是系数模$p$。

然后$R_p$中的取余操作和$R$的类似，不再累赘。$R_q$和$R_p$类似，只是模数不同。

以上的$N$、$p$和$q$是NTRU的公开参数，在[HPS14]中的参数要求是，$N$为素数，且

$$\rm{gcd}(N, q) = \rm{gcd}(p, q) = 1$$

以下更详细的参数设置建议摘抄自[HPS17]，大概意思是：$p$一般取$p=3$，$q$为了加快运算一般取$2$的幂次方（盲猜是二进制有利于计算机优化），$N$同样取素数，不过某些特殊版本的基于理想格的NTRU会取形如$N=2^n$，然后模数取$x^N+1$，这里超纲了，略。

三元多项式和密钥生成·

接下来会说到一个叫$\mathcal{T}$的函数：

$\mathcal{T}$的输入为两个整数$d_1$和$d_2$，输出为一个三元多项式（Ternary Polynomial），三元即$(-1, 0, 1)$，大概意思是，$\mathcal{T}$函数会采样一个符合条件：有$d_1$个项系数为$1$、有$d_2$个项系数为$-1$，其余项系数为$0$（即没有）的多项式，且这个多项式落在$R$上。

接下来利用$\mathcal{T}$采样密钥，首先是私钥，我就直接上图不再码一遍了：

其中的$d$也是公开参数（上面也有说了），$f(x)$和$g(x)$是两个主要的私钥（甚至可以把$g(x)$看作一个随机数），落在$R$中（因为$\mathcal{T}$的返回值落在$R$中，先记住，后面会用到），$F_q(x)$和$F_q(x)$分别是$f(x)$在$R_q$和$R_p$上的逆元，这里写出来的意思是，把$F_q(x)$和$F_q(x)$存储起来可以加快运算速度，因为计算多项式环的逆元需要一段时间（虽然也不是很久）。

多嘴说一句，$f(x)$取自$\mathcal{T}(d+1, d)$是因为需要$f(x)$可逆，书中有提到$\mathcal{T}(d, d)$的不可逆，也可以自己推一遍。

这里隐藏的一个信息是，$R$上的多项式可以转换到$R_q$或$R_p$中，系数模$q$或者模$p$而已，挺显然的，略。

然后计算公钥：

换一种写法其实也就是：

$$h(x) \equiv f(x)^{-1} · g(x) \ \text{in } R_q$$

Center-lift和加解密·

首先说Center-lift，上面说了，$R$上的多项式可以转换到$R_q$或$R_p$中，而Center-lift则是把$R_q$或$R_p$中的多项式转换回$R$中，而且使得多项式系数的绝对值最小（相比于其他的转换方式）。

Center-lift的定义可以看[HSP14]的7.9节，主要是针对多项式系数的操作，可以和补码类比。

上面假设是$R_q$多项式的Center-lift，即$R_q$转换到$R$。上图的$a(x)$为$R_q$上的一个多项式，$a'(x)$为其Center-lift到$R$后的结果，$a_i$为$a(x)$的$i$次项系数，$a_i'$为$a'(x)$的$i$次项系数。

Center-lift后的结果是，所有的系数$a_i'$会落在区间$(-\frac{q}{2}, \frac{q}{2}]$，而且还能保证$a_i' \equiv a_i \pmod q$。

Center-lift的方法也不难，和转补码类似，在$\frac{q}{2}$砍一半，小于等于$\frac{q}{2}$的不动，大于$\frac{q}{2}$的平移到$(-\frac{q}{2}, 0)$，也就是：

$$a_i' = \begin{cases} a_i, & \text {if $0 \le a_i \le \frac{q}{2}$} \\ a_i - q, & \text {if $\frac{q}{2} < a_i < q $} \end{cases}$$

检验一下，上面的划分可以覆盖整个$\mathbb{Z}_q$，当$0 \le a_i \le \frac{q}{2}$时显然$a_i' \equiv a_i \pmod q$，而且落在$(-\frac{q}{2}, \frac{q}{2}]$；$\frac{q}{2} < a_i < q$时，$a_i' \equiv a_i - q \equiv a_i - 0 \equiv a_i \pmod q$，由于$a_i$落在$(\frac{q}{2}, q)$，所以$a_i' \equiv a_i - q$落在$(\frac{q}{2}-q, q-q)$，也即$(-\frac{q}{2}, 0)$，自然落在$(-\frac{q}{2}, \frac{q}{2}]$，检验通过。

然后接着看加密，明文空间是$R_p$做Center-lift后的空间，也即在$R$上，系数取值落在$(-\frac{p}{2}, \frac{p}{2}]$的空间，加密使用的随机数$r(x)$在$\mathcal{T}(d, d)$中采样，然后加密操作就是下图的公式，密文是$e(x)$。

在继续解密操作前，先分析一下密文的结构。

首先如果要解密的话，其实只用把$p·h(x)·r(x)$这一项去除，先剧透一下，由于$p \equiv 0 \ \text{in } R_p$，所以直观上把$e(x)$放入$R_p$中就可以把$p·h(x)·r(x)$去除，而由于明文空间是$R_p$做Center-lift后的空间，所以把$m(x) \ \text{in }R_q$放入$R_p$中并不会改变$m(x)$的结构，即可以恢复明文。

剩下的问题是我其实并不能保证$[e(x) \pmod q] \equiv e(x) \pmod p$，除非$q = kp$（这种情况在前几天讲OU98时有讲过），但因为$\rm{gcd}(p, q) = 1$，所以这种情况并不存在。

这样的栗子可以举很多，可以直接看整数的栗子（反正也是模在多项式系数上），设$e=65537$、$q=512$、$p=3$，计算可得

$$\begin{aligned} (e \pmod q) \pmod p = (65537 \pmod {512}) \pmod 3 = 1 \pmod 3 &= 1 \\ e \pmod p = 65537 \pmod 3 &= 2 \end{aligned}$$

显然不等，也即$R_q$不能直接转换到$R_p$上。

但是前面说过，$R$可以转换到$R_p$上，所以可以考虑先把$e(x)$转换（Center-lift）到$R$上，然后再转到$R_p$上。

但新的问题是，直接把$R_q$上的$e(x)$转到$R$上，其结果不一定是原来$R$上的$e(x)$，举个整数域上的栗子即$65537 \pmod {512} = 1 \ne 65537$，除了一种情况，即把$e(x)$放在$R$上运算后的系数本来就落在$(-\frac{q}{2}, \frac{q}{2}]$，也即$R_q$上的元素做Center-lift后的区间。

在讲如何把$e(x)$系数转化到$(-\frac{q}{2}, \frac{q}{2}]$前，可能先需要了解一下多项式的乘法。

多项式卷积乘法·

在继续讲解密思路前，先“简要”介绍一下多项式卷积。

在这篇我曾经写过，多项式的卷积乘法可以看成一个矩阵操作，这里多嘴推导一下这个矩阵是怎么来的，如果不关心推导则可以跳过。

下面假设$f(x)$和$g(x)$在$R$中相乘（假设而已），先把多项式表述为：

$$f(x) \equiv \sum^{N-1}_{i=0} f_i x^i \\ g(x) \equiv \sum^{N-1}_{i=0} g_i x^i$$

那么有（参考多项式乘法，用分配律推也行）：

$$\begin{aligned} f(x) · g(x) &\equiv \sum^{N-1}_{i=0} (f_i x^i \sum^{N-1}_{j=0} g_j x^j) \\ &\equiv \sum^{N-1}_{i=0} \sum^{N-1}_{j=0} f_i x^i g_j x^j \\ &\equiv \sum^{N-1}_{i=0} \sum^{N-1}_{j=0} f_i g_j x^{i+j} \ \text{(in $R$)} \end{aligned}$$

由于$f(x) · g(x)$的结果肯定也是个多项式（封闭性），所以先把上面结构调整到像一个多项式，即合并次数相同的项（注意$f(x)$和$g(x)$最高项只能是$x^{N-1}$，所以不考虑模的时候乘起来最高项只能是$x^{N-1} · x^{N-1} = x^{2(N - 1)}$，然后小于$N$次的项和大于等于$N$次的项分开处理）：

$$\begin{aligned} f(x) · g(x) &\equiv \sum^{N-1}_{i=0} \sum^{N-1}_{j=0} f_i g_j x^{i+j} \\ \\ &\equiv \sum^{N-1}_{k=0} ((\sum^{k}_{i=0} f_{i} g_{k-i}) · x^k) + \sum^{2(N-1)}_{k=N} ((\sum^{N-1}_{i=k-(N-1)} f_{i} g_{k-i}) · x^k) \ \text{(in $R$)} \end{aligned}$$

最开始讲环的时候说到，$R$是模$x^N-1$的，所以$x^N \equiv 1 \equiv x^0 \ \text{(in }R \text{)}$，所以有

$$x^{N + i} \equiv x^i \ \text{(in $R$)}$$

即未知数$x$的指数部分需要模$N$，所以可以继续化简：

$$\begin{aligned} f(x) · g(x) &\equiv \sum^{N-1}_{k=0} ((\sum^{k}_{i=0} f_{i} g_{k-i}) · x^k) + \sum^{2(N-1)}_{k=N} ((\sum^{N-1}_{i=k-(N-1)} f_{i} g_{k-i}) · x^{k-N}) \\ &\equiv \sum^{N-1}_{k=0} ((\sum^{k}_{i=0} f_{i} g_{k-i}) · x^k) + \sum^{N-2}_{k=0} ((\sum^{N-1}_{i=(k+N)-(N-1)} f_{i} g_{(k+N)-i}) · x^k) \\ &\equiv \sum^{N-1}_{k=0} ((\sum^{k}_{i=0} f_{i} g_{k-i}) · x^k) + \sum^{N-1}_{k=0} ((\sum^{N-1}_{i=k+1} f_{i} g_{k+N-i}) · x^k) \\ &\equiv \sum^{N-1}_{k=0} (\sum^{k}_{i=0} f_{i} g_{k-i} + \sum^{N-1}_{i=k+1} f_{i} g_{k+N-i}) · x^k \\ &\equiv \sum^{N-1}_{k=0} (\sum^{N-1}_{i=0} f_{i} g_{k-i \pmod N}) · x^k \ \text{(in $R$)} \end{aligned}$$

其中的$\sum^{N-1}_{i=0} f_{i} g_{k-i \pmod N}$即为$f(x) · g(x)$的$k$次项系数。

粗略检验一下正确性，设$f(x)=x^2+2x + 3$、$g(x) = 3x^2 + 2x + 1$、$N=3$，则：

$$\begin{aligned} f(x) · g(x) &\equiv (x^2+2x + 3) · (3x^2 + 2x + 1) \\ &\equiv 3 x^4 + 8 x^3 + 14 x^2 + 8 x + 3 \\ &\equiv 3x + 8 + 14x^2 + 8x + 3 \\ &\equiv 14x^2 + 11x + 11 \ \text{(in $R$)} \end{aligned}$$

$$\begin{aligned} &\sum^{N-1}_{k=0} (\sum^{N-1}_{i=0} f_{i} g_{k-i \pmod N}) · x^k \\ \equiv &\sum^{2}_{k=0} (\sum^{2}_{i=0} f_{i} g_{k-i \pmod 3}) · x^k \\ \equiv &(\sum^{2}_{i=0} f_{i} g_{0-i \pmod 3}) · x^0 + (\sum^{2}_{i=0} f_{i} g_{1-i \pmod 3}) · x^1 + (\sum^{2}_{i=0} f_{i} g_{2-i \pmod 3}) · x^2 \\ \equiv &(f_0 g_0 + f_1 g_2 + f_2 g_1) · x^0 + (f_0 g_1 + f_1 g_0 + f_2 g_2) · x^1 + (f_0 g_2 + f_1 g_1 + f_2 g_0) · x^2 \\ \equiv &(3·1 + 2·3 + 1·2) · x^0 + (3·2 + 2·1 + 1·3) · x^1 + (3·3 + 2·2 + 1·1) · x^2 \\ \equiv &14x^2 + 11x^1 + 11x^0 \\ \equiv &14x^2 + 11x + 11 \ \text{(in $R$)} \end{aligned}$$

检验通过。

以下用矩阵的形式表达$\sum^{N-1}_{k=0} (\sum^{N-1}_{i=0} f_{i} g_{k-i \pmod N}) · x^k$，姑且记$f(x)·g(x)$的$i$次项系数为$\lambda_i$，即为

$$(f_0, f_1, ..., f_{N-1}) · \begin{pmatrix} g_0 & g_1 & g_2 & \cdots & g_{N-1} \\ g_{N-1} & g_0 & g_1 & \cdots & g_{N-2} \\ g_{N-2} & g_{N-1} & g_0 & \cdots & g_{N-3} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ g_1 & g_2 & g_3 & \cdots & g_0 \\ \end{pmatrix} \\ = (\lambda_0, \lambda_1, ..., \lambda_{N-1})\ \ \text{(in $R$)}$$

解密与参数关系计算·

首先直接贴解密过程，

公式推导我也懒得再码一遍了，直接截图：

现在的目标是要把$e(x)$的系数转化到$(-\frac{q}{2}, \frac{q}{2}]$区间，而观察$e(x)$的结构可发现，要达成这个目标最大的阻碍是$h(x)$，因为$h(x) \equiv f(x)^{-1} · g(x) \ \text{in } R_q$，其中的$f(x)^{-1}$取逆操作会把系数“打乱”，从而产生很大（$q$规模）的系数，所以需要想方法消去。

消去方法如上面$a(x)$的推导，乘上一个$f(x)$，把$h(x)$转换成$g(x)$，$g(x) \in \mathcal{T}(d, d)$，其系数只会是小系数$-1$、$0$或$1$。

虽然消去$h(x)$，但其实还不能保证$a(x)$的绝对值系数严格落在$(-\frac{q}{2}, \frac{q}{2}]$，所以接下来需要先计算$a(x)$的最大和最小系数，计算方法稍微引用下原文：

可以把$a(x)$分成两部分，即“+”分割的$p · g(x) · r(x)$和$f(x) · m(x)$。

首先看$p · g(x) · r(x)$的最大和最小系数，由于$p$是常数，所以可以先看$g(x) · r(x)$，翻看上面内容，$g(x)$和$r(x)$都采样自$\mathcal{T}(d, d)$，即只有$d$个系数为$1$的项和$d$个系数为$-1$的项，其余项系数为$0$。

上一节已经推出了，$\sum^{N-1}_{i=0} g_{i} r_{k-i \pmod N}$为$g(x) · r(x)$的$k$次项系数，由于$g_{i} r_{k-i \pmod N}$只会在$g_{i}$和$r_{k-i \pmod N}$都取$1$或者都取$-1$时可以取得最大值$1$，所以在拥有最多的$g_{i} r_{k-i \pmod N}$出现最大值$1$的情况下$g(x) · r(x)$的$k$次项系数出现最大值，这个情况即是：值为$1$的$g_{i}$刚好匹配上值为$1$的$r_{k-i \pmod N}$、值为$-1$的$g_{i}$刚好匹配上值为$-1$的$r_{k-i \pmod N}$、且值为$0$的$g_{i}$刚好匹配上值为$0$的$r_{k-i \pmod N}$的情况，产生的最大值是$2d$。

再把常数$p$考虑进去，即$p · g(x) · r(x)$的最大值是$p·2d$。

类似地，当$1$和$-1$匹配上的时候，$g_{i} r_{k-i \pmod N}$出现最小值$-1$，即得$p · g(x) · r(x)$的最小值是$-p·2d$。

再来看$f(x) · m(x)$得最大和最小系数，$f(x)$采样自$\mathcal{T}(d+1, d)$，即有$d+1$个项系数为$1$、有$d$个项系数为$-1$、其余项为$0$；$m(x)$的系数落在$(-\frac{p}{2}, \frac{p}{2}]$，即$R_p$做Center-lift后的区间。

类似地，$\sum^{N-1}_{i=0} f_{i} m_{k-i \pmod N}$为$f(x) · m(x)$的$k$次项系数，$f_{i} m_{k-i \pmod N}$只会在$f_{i}$取$1$、$m_{k-i \pmod N}$取$\frac{p}{2}$时和在$f_{i}$取$-1$、$m_{k-i \pmod N}$取$-\frac{p}{2}$（虽然取不到，但可以用来计算界）时取得最大值$\frac{p}{2}$，这些情况总共可以出现$(d+1)+d$次（$f(x)$中$1$的个数加上$-1$的个数），所以$f(x) · m(x)$的系数最大值是$(2d+1) · \frac{p}{2}$。

再类似地，在$f_{i}$取$1$、$m_{k-i \pmod N}$取$-\frac{p}{2}$时和在$f_{i}$取$-1$、$m_{k-i \pmod N}$取$\frac{p}{2}$时，$f_{i} m_{k-i \pmod N}$取得最小值$-\frac{p}{2}$，总可出现$(2d+1)$次，所以所以$f(x) · m(x)$的系数最小值是$-(2d+1) · \frac{p}{2}$。

最后$a(x)$的最大系数就是$p · g(x) · r(x)$和$f(x) · m(x)$两部分的最大系数之和，即

$$p·2d + (2d+1) · \frac{p}{2} = 3dp + \frac{p}{2} = (3d + \frac{1}{2}) · p$$

同理，最小系数是$-(3d + \frac{1}{2}) · p$。（希望到这里还没看晕，逃）

接下来，要保证$a(x)$的系数落在$(-\frac{q}{2}, \frac{q}{2}]$，只需要保证其最大系数严格小于$\frac{q}{2}$且最小系数严格大于$-\frac{q}{2}$即可，（经过上面计算可发现其实这两个是等价的，多了个负号而已），所以即需要保证：

$$(3d + \frac{1}{2}) · p < \frac{q}{2}$$

化简也即：

$$(6d+1)·p < q$$

即需要在设置四个公开参数时保证以上关系，才能让$a(x)$正确地转换到$R$上，保证解密的正确性。

接着按前文说的，现在$a(x)$在$R$上，可以转换到$R_p$上以消除$p · g(x) · r(x)$：

$$a(x) \equiv p · g(x) · r(x) + f(x) · m(x) \equiv f(x) · m(x) \ \text{(in $R_p$)}$$

为了恢复出$m(x)$还需要消去$f(x)$，这直接乘上$f^{-1}(x)$即可：

$$b(x) \equiv F_p(x) · a(x) \equiv f^{-1}(x) · f(x) · m(x) \equiv m(x) \ \text{(in $R_p$)}$$

到这可以已经解密出$m(x)$，但这个$m(x)$落在$R_p$，即系数取值在$[0, p)$，而实际的$m(x)$取值应该是在$(-\frac{p}{2}, \frac{p}{2}]$，所以最后还要把$b(x)$做一次Center-lift才解出真正的$m(x)$。

总结·

公开参数：$(N, p, q, d)$，其中$N$是素数、$p$一般取$3$、$q$一般取$2$的幂，还需要保证$\rm{gcd}(N, q) = \rm{gcd}(p, q) = 1$，和$(6d+1)·p < q$；

密钥生成：采样$f(x) \overset{\$}{\leftarrow} \mathcal{T}(d+1, d)$、$g(x) \overset{\$}{\leftarrow} \mathcal{T}(d, d)$，计算$F_q \equiv f^{-1}(x) \ \text{(in }R_q \text{)}$和$F_p \equiv f^{-1}(x) \ \text{(in }R_p \text{)}$，计算公钥$h(x) \equiv F_q(x) g(x) \ \text{(in }R_q \text{)}$。

• 私钥为：$(f(x), g(x), F_q(x), F_p(x))$
• 公钥为：$h(x)$

加密：明文$m(x)$的系数需落在$(-\frac{p}{2}, \frac{p}{2}]$（虽然很奇怪下面表中说明文取自$R_p$），采样随机数$r(x) \overset{\$}{\leftarrow} \mathcal{T}(d, d)$，密文为$e(x)\equiv ph(x)r(x) + m(x) \ \text{(in }R_q \text{)}$；

解密：计算$a(x) \equiv f(x)e(x) \ \text{(in }R_q \text{)}$并做Center-lift到$a(x) \in R$，计算$m(x) \equiv F_p(x) a(x) \ \text{(in }R_q \text{)}$，最后把$m(x)$做Center-lift到$R$（如果明文取自$R_p$则不需要这一步）。

参考代码·

参照上面理论部分写了个代码，其实我在很久以前就写过一个NTRU的代码，但因为穷拿去投题了，所以有保密协议就不能发，这次代码的加了很多骚操作，整体来说也更美观，所以感觉还是值得发一下。

首先是三个环$R$、$R_p$和$R_q$，需要先做出$\mathbb{Z}[x]$、$(\mathbb{Z}/p\mathbb{Z})[x]$和$(\mathbb{Z}/q\mathbb{Z})[x]$，在Sage代码中写作：

R_  = PolynomialRing(ZZ,'x')
Rp_ = PolynomialRing(Zmod(p),'xp')
Rq_ = PolynomialRing(Zmod(q),'xq')

其中为了防止混淆，$(\mathbb{Z}/p\mathbb{Z})[x]$和$(\mathbb{Z}/q\mathbb{Z})[x]$的未知数在代码中我称作xp和xq。

然后使用上面三个东西做商环（模$x^N-1$）就得到三个环$R$、$R_p$和$R_q$：

R  = R_.quotient(x^N - 1, 'y')
Rp = Rp_.quotient(xp^N - 1, 'yp')
Rq = Rq_.quotient(xq^N - 1, 'yq')

其中也是为了防混淆，我把$R$、$R_p$和$R_q$上的未知数称作y、yp和yq。

然后采样三元多项式的函数$\mathcal{T}$，我选择先固定$d_1$个系数$1$和$d_2$个系数$-1$，然后再用shuffle将其打乱以获得随机的输出，然后要注意$\mathcal{T}$的输出落在$R$（毕竟有负数）：

def T(self, d1, d2):
  assert self.N >= d1+d2
  t = [1]*d1 + [-1]*d2 + [0]*(self.N-d1-d2)
  shuffle(t)
  return self.R(t)

Center-lift函数基本照抄理论部分的公式就可以了，但由于作为函数我并不知道需要Lift的是$R_p$环还是$R_q$环，所以需要用“曲线救国”的方法在输入中提取模数（估计有更好的方法，懒）：

def lift(self, fx):
  mod = Integer(fx.base_ring()(-1)) + 1  # emmm
  return self.R([Integer(x)-mod if x > mod//2 else x for x in list(fx)])

然后是密钥生成，首先$f(x)$和$g(x)$直接用$\mathcal{T}$采样即可。$F_p$的计算，由于在$R_p$上，而$p$是素数，所以用Sage可以很方便地求逆：

Fp = self.Rp(list(fx)) ^ (-1)

上面需要先把fx转换到Rp上再做求逆，而由于前面设置的未知数名称不一致，不能直接用Rp(fx)做转换，曲线救国，先用list(fx)提取fx的系数，然后用系数转到Rp。

$F_q$的计算则有点复杂，由于$q$不为素数所以不能直接用Sage像上面那样求逆，目前网上查到的流行做法如这个教程的invertmodpowerof2做递归求逆，但是我后来想到了一种更美观的“曲线救国”方法。

参考整数域上的求逆，比如要求$a^{-1} \pmod n$，除了用egcd求逆外，还有一种方法是（借助欧拉定理）：

$$a^{\varphi(n)-1} \equiv a^{\varphi(n)} a^{-1} \equiv 1 · a^{-1} \equiv a^{-1} \pmod n$$

其中的$\varphi(n)$即$\mathbb{Z}_n^*$的阶。

所以只要求出$F_q$的阶即可利用类似方法求逆，问题是如何求$F_q$的阶。

经过计算加实验~~（原理未明，留坑）~~，发现$f(x)$在$F_q$的阶（$q$为$2$的幂次）为：

$$\varphi(q) = q^{N} - q$$

的因子。

PS：这里我取了最大值，即以上不是真正符合阶的定义，但是阶的某个倍数，所以说其阶是上面式子的一个因子，如果有方法可以分解上式则可能可以找到真正的阶，但在$q$不大的情况下找到真正的阶其实并不能显著加速求逆的效率，所以可以选择直接使用$\varphi(q)$。

而$f(x)$在$F_p$的阶为（$p$为素数）：

$$\varphi(p) = p^{N} - p$$

的因子。这个结果和之前求$GL(n, \mathbb{F}_p)$阶的结果类似，毕竟$p$为素数时，两个东西同构（如果我没记错的话，逃）。

PS：（2024.01.03更新）这里求阶的方法其实和RSA中求$\varphi$的方法类似，首先需要把所模的多项式分解为不可约的多项式，然后再分别求模这些不可约多项式的子环的阶，最后乘起来就是所求的真正的阶。但是这样算出来的阶会非常复杂，而$p^{N} - p$又刚好阴差阳错地是这些阶的一个倍数，所以还是直接用$p^{N} - p$为好（逃

另外，若$p$和$q$不按[HPS14]的说明选择，根据中国剩余定理（CRT），假设$p = \sum_i p_i^{k_i}$，则$f(x)$在$F_p$的阶为：

$$\prod_i (p_i^{k_iN} - p_i^{k_i})$$

综上，通过计算

$$F_p \equiv f(x)^{\varphi(p)-1} \equiv f^{-1}(x) \ \text{(in $R_p$)} \\ F_q \equiv f(x)^{\varphi(q)-1} \equiv f^{-1}(x) \ \text{(in $R_q$)}$$

即可算出$F_p$和$F_q$。

然后加密好像没啥可说的，只是为了统一，我把返回值转成字符串再输出，这样在输进解密函数时也不需要考虑类型问题。

解密函数也没啥好说，关注Center-lift的时机即可。

最后的参考代码：

# Sage

# Ref: https://www.osgeo.cn/sagemath/constructions/rings.html
class NTRU:
  def __init__(self, N, p, q, d):
    self.debug = False

    assert q > (6*d+1)*p
    assert is_prime(N)
    assert gcd(N, q) == 1 and gcd(p, q) == 1
    self.N = N
    self.p = p
    self.q = q
    self.d = d
  
    self.R_  = PolynomialRing(ZZ,'x')
    self.Rp_ = PolynomialRing(Zmod(p),'xp')
    self.Rq_ = PolynomialRing(Zmod(q),'xq')
    x = self.R_.gen()
    xp = self.Rp_.gen()
    xq = self.Rq_.gen()
    self.R  = self.R_.quotient(x^N - 1, 'y')
    self.Rp = self.Rp_.quotient(xp^N - 1, 'yp')
    self.Rq = self.Rq_.quotient(xq^N - 1, 'yq')

    # order check in keyGen
    #self.RpOrder = self.p^(self.N - 1) - 1
    #self.RqOrder = (self.q^self.N - self.q) // (self.q-1)
    self.RpOrder = self.p^self.N - self.p
    self.RqOrder = self.q^self.N - self.q

    self.sk, self.pk = self.keyGen()


  def test(self):
    assert self.debug == True
    pass


  def T(self, d1, d2):
    assert self.N >= d1+d2
    t = [1]*d1 + [-1]*d2 + [0]*(self.N-d1-d2)
    shuffle(t)
    return self.R(t)

  # center lift
  def lift(self, fx):
    mod = Integer(fx.base_ring()(-1)) + 1  # emmm
    return self.R([Integer(x)-mod if x > mod//2 else x for x in list(fx)])


  def keyGen(self):
    fx = self.T(self.d+1, self.d)
    gx = self.T(self.d, self.d)

    Fp = self.Rp(list(fx)) ^ (-1)                           # list emmm
    assert pow(self.Rp(list(fx)), self.RpOrder-1) == Fp     # order checked
    assert self.Rp(list(fx)) * Fp == 1                
    
    # Fq = self.Rq(fx) ^ (-1)   # wasted
    Fq = pow(self.Rq(list(fx)), self.RqOrder - 1)     # invert
    assert self.Rq(list(fx)) * Fq == 1                # order checked
    
    hx = Fq * self.Rq(list(gx))

    sk = (fx, gx, Fp, Fq, hx)
    pk = hx
    return sk, pk


  def setKey(self, fx, gx):
    assert type(fx) == type('x^2 + 1')  # e.g.
    assert type(gx) == type('x^2 - 1')  # emmm

    try:
      fx = self.R(fx)
      gx = self.R(gx)

      Fp = self.Rp(list(fx)) ^ (-1)
      Fq = pow(self.Rq(list(fx)), self.RqOrder - 1)
      hx = Fq * self.Rq(list(gx))

      self.sk = (fx, gx, Fp, Fq, hx)
      self.pk = hx
      return True
    except:
      return False

  
  def getKey(self):
    ssk = (
          str(self.R_(list(self.sk[0]))),   # fx
          str(self.R_(list(self.sk[1])))    # gx
        )
    spk = str(self.Rq_(list(self.pk)))      # hx
    return ssk, spk
   

  def encrypt(self, m):
    assert type(m) == type('x^2 + 1') # e.g.
    assert self.pk != None
    hx = self.pk
    mx = self.R(m)
    mx = self.Rp(list(mx))              # change m to Rp, TODO: assert m in Rp
    mx = self.Rq(list(mx))              # change m to Rq

    rx = self.T(self.d, self.d)
    rx = self.Rq(list(rx))
    

    e = self.p * rx * hx + mx
    #return e
    return str(self.Rq_(list(e)))


  def decrypt(self, e):
    assert type(e) == type('xq^2 - 1')  # e.g.
    assert self.sk != None
    fx, gx, Fp, Fq, hx = self.sk

    e = self.Rq(e)
    ax = self.Rq(list(fx)) * e
    a = self.lift(ax)                   # center lift
    bx = Fp * self.Rp(list(a))
    b = self.lift(bx)
    
    #return bx
    return str(self.R_(list(b)))
    


if __name__ == '__main__':
  mm = '-x^2 + x + 1'
  ntru = NTRU(N=11, p=3, q=512, d=3)
  #ntru.setKey('xp^2+1', 'xq^2-1')
  
  print('keyGen check:')
  sk, pk = ntru.getKey()
  print("fx = '%s'" % sk[0])
  print("gx = '%s'" % sk[1])
  print("hx = '%s'" % pk)
  
  print('\nencrypt/decrypt check:')
  e = ntru.encrypt(mm)
  print("e = '%s'" % e)
  m = ntru.decrypt(e)
  print(m)
  assert m == mm
  print(m)

  print('\ncheck setKey:')
  fx = 'x^10 + x^9 - x^8 - x^5 + x^4 + x - 1'
  gx = '-x^10 + x^9 - x^6 - x^5 + x^4 + 1'
  hx = '357*xq^10 + 156*xq^9 + 22*xq^8 + 467*xq^7 + 356*xq^6 + 23*xq^5 + 422*xq^4 + 490*xq^3 + 200*xq^2 + 201*xq + 378'
  e = '286*xq^10 + 336*xq^9 + 355*xq^8 + 220*xq^7 + 330*xq^6 + 198*xq^5 + 182*xq^4 + 443*xq^3 + 454*xq^2 + 45*xq + 227'
  ntru.setKey(fx, gx)
  m = ntru.decrypt(e)
  assert m == mm
  print(m)

攻击方法·

下面说一下[HPS14]里提到的两种攻击方法。

小密钥空间·

[HPS14]的7.10.2中提到：

即$N$和$d$的取值不合理的话，会导致$f(x)$的取值空间过小，从而可以被攻击者枚举出密钥。

这个在参数设置上注意就好了，做题的话看见$N$和$d$过小可以考虑直接枚举。

格规约攻击·

这里参考[HPS14]的7.11的内容，主要关注公钥的生成：

$$h(x) \equiv f(x)^{-1} · g(x) \ \text{in } R_q$$

把模数去除，参考[HPS14]的写法即存在一个多项式$u(x)$使得：

$$f(x) · h(x) - q · u(x) = g(x)$$

写成矩阵形式也即（如果熟悉格规约的话，会把已知的放进矩阵）：

$$(f(x), -u(x)) \begin{bmatrix} 1 & h(x) \\ 0 & q \\ \end{bmatrix} = (f(x), g(x))$$

这个只是一个写着方便的表述，实际上$f(x)$、$g(x)$、$h(x)$和$u(x)$都是多项式，不能这样简单地占一个位置，应该

• 多项式相乘：用前面说的多项式卷积乘法的矩阵写法；
• 多项式数乘：用多项式的系数向量和对角线上为该常数的对角矩阵相乘；

这里我就直接抄书了：

用书中的简化写法是（为了混淆$h(x)$我用了$H$，$I$是单位矩阵）：

$$M_h^{\rm{NTRU}} = \begin{bmatrix} \begin{array}{l|l} I & H \\ \hline 0 & qI \end{array} \end{bmatrix}$$

存在关系（记$f$为$f(x)$的系数向量，记$g$为$g(x)$的系数向量）：

$$(f | -u) · M_h^{\rm{NTRU}} = (f | g)$$

直观上$f$和$g$上元素的绝对值最大是$1$，所以$(f | g)$是“小”向量，用LLL对$M_h^{\rm{NTRU}}$规约即可出$(f | g)$，这里先计算一下，我就直接借用[HPS14]的计算（懒）：

但实际操作的情况是，LLL实际上解的是apprSVP，当矩阵规模变大时，求出$(f | g)$的能力会变小，所以只要设置足够大的$N$即可防止这类攻击。

贴个攻击参考代码：

# Sage

def matrix_overview(BB):
    for ii in range(BB.dimensions()[0]):
        a = ('%02d ' % ii)
        for jj in range(BB.dimensions()[1]):
            if BB[ii, jj] == 0:
                a += ' '
            else:
                a += 'X'
            if BB.dimensions()[0] < 60:
                a += ' '
        print(a)

# cp NTRU.sage.py NTRU.py
from NTRU import NTRU

N = 11
q = 512
p = 3
d = 3
hx = '357*xq^10 + 156*xq^9 + 22*xq^8 + 467*xq^7 + 356*xq^6 + 23*xq^5 + 422*xq^4 + 490*xq^3 + 200*xq^2 + 201*xq + 378'
e = '286*xq^10 + 336*xq^9 + 355*xq^8 + 220*xq^7 + 330*xq^6 + 198*xq^5 + 182*xq^4 + 443*xq^3 + 454*xq^2 + 45*xq + 227'

Rq_ = PolynomialRing(Zmod(q),'xq')
h = vector(list(Rq_(hx)))
print(h)

M = matrix(ZZ, 2*N)
for i in range(N):
  M[i, i]     = 1
  M[N+i, N+i] = q
  for j in range(N):
    M[i, N+j] = h[(j-i) % N]
matrix_overview(M)
#print(M)

L = M.LLL()
#L = M.BKZ(block_size=32)

def inT(f, d1, d2, N):
  fl = list(f)
  c1 = fl.count(1)
  c_1 = fl.count(-1)
  c0 = fl.count(0)
  return c1==d1 and c_1==d2 and c1+c0+c_1 == N

R_  = PolynomialRing(ZZ,'x')
ntru = NTRU(N=N, p=p, q=q, d=d)
for i in range(N):
  fg = L[i]
  f = vector(ZZ, fg[:N])
  g = vector(ZZ, fg[N:])

  if inT(f, d+1, d, N):
    pass
  elif inT(-f, d+1, d, N):
    f = -f
  else:
    continue
    
  if inT(g, d, d, N):
    pass
  elif inT(-g, d, d, N):
    g = -g	# duoyu
  else:
    continue

  print('Trying in i = %d' % i)
  fx = str(R_(list(f)))
  gx = str(R_(list(g)))
  print('f = %s' % fx)
  print('g = %s' % gx)
  ntru.setKey(fx, gx)
  m = ntru.decrypt(e)
  print('m = %s' % m)

  print('----------------\n')

有一个尴尬的情况是，$M_h^{\rm{NTRU}}$是一个N-Gap的格，也即LLL/BKZ规约后的矩阵中，前N行向量的规模是相近的，这会导致LLL/BKZ规约后的第一行不一定是$(f | g)$，当然也会有$(f | g)$不是最短向量的情况。

曲线救国的方法是，把前N行向量都试一遍，先检测其是否落在$\mathcal{T}(d+1, d)$，再尝试解密。

另外，实验测出有多个多个$f(x)$都可以实现解密的情况，合理怀疑一个公钥$h(x)$可以对应多个私钥$f(x)$，也就是有可能上面解出来的前$N$行都是对的，emmmm。