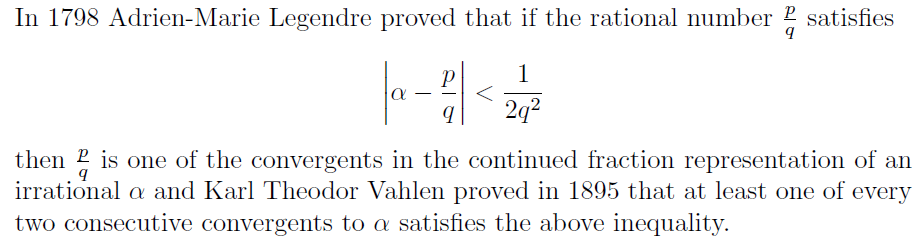最近复习了一下经典的攻击

一直以来看到Wiener攻击的攻击范围都是d<13n1/4d < \frac{1}{3}n^{1/4}，翻回相关的一些论文，发现原来在证明Wiener攻击的界时都会假设两个东西：pp和qq的比特长度相同，和e≈Ne \approx N

在这些假设下，界的计算会简单很多，但是所算出来的其实是一个基于这两种假设的特殊情况的界，并没考虑ee和pp的影响

在我以前写过的这篇和这篇文章中都提到，用格规约和连分数去打小解密指数攻击其实是等价的，然后用格的方法推出攻击的界应该是ped2<N2ped^2 < N^2，其中pp为较大的素数，即p≥qp \ge q

但是格毕竟是格，连分数才是连分数，所以今天用连分数的方法推了一个类似的结果，在这里记录一下

正文·

首先Wiener攻击或者目前基于连分数的攻击其原理都是以下一条定理

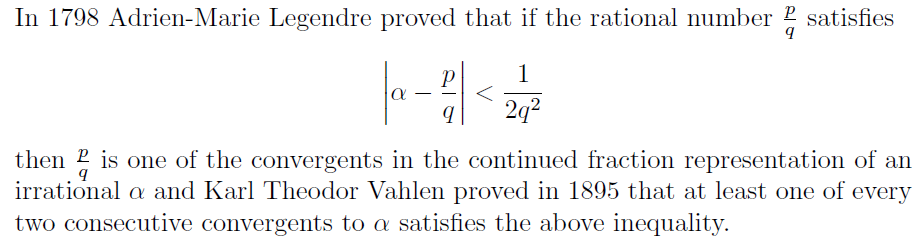
代入到RSA中，密钥生成过程可得ed≡1(modφ)ed \equiv 1 \pmod {\varphi}，也就是存在kk使得

ed−kφ=1ed - k \varphi = 1

可知

φ=(p−1)(q−1)=N−(p+q−1)\varphi = (p-1)(q-1) = N - (p + q - 1)

代入上式就是

ed−kN=1−k(p+q−1)ed - kN = 1 - k(p + q - 1)

为了凑到以上定理，对式子等号左右同除以dNdN，然后取绝对值

∣eN−kd∣=k(p+q−1)−1dN\left| \frac{e}{N} - \frac{k}{d} \right| = \frac{k(p + q - 1) - 1}{dN}

如果想要利用该定理，在这里需要

k(p+q−1)−1dN<12d2\frac{k(p + q - 1) - 1}{dN} < \frac{1}{2d^2}

令pp是较大的一个素数，也即p≥qp \ge q，可得p+q−1<2pp + q - 1 < 2p，代入到上式中，再消一下元就可以得到需要

2kp<N2d+12kp < \frac{N}{2d} + 1

接下来再消去麻烦的kk，由于k=ed−1φk = \frac{ed-1}{\varphi}，而且φ=N−(p+q−1)>N−2p\varphi = N - (p+q-1) > N - 2p，所以

k<ed−1N−2pk < \frac{ed-1}{N-2p}

代入，即得到需要

2⋅ed−1N−2p⋅p<N2d+12 \cdot \frac{ed-1}{N-2p} \cdot p < \frac{N}{2d} + 1

然后就是对这个式子化简

ed−1q−2<N4d+12ed−1q−2<N+2d4d4ed2−4d<(q−2)(N+2d)=qN−2N+2qd−4d4ed2<qN−2N+2qd\frac{ed-1}{q-2} < \frac{N}{4d} + \frac{1}{2} \\ \frac{ed-1}{q-2} < \frac{N + 2d}{4d} \\ 4ed^2 - 4d < (q - 2) (N + 2d) = qN - 2N + 2qd - 4d \\ 4ed^2 < qN - 2N + 2qd

左右乘个pp把qq消去，就得到

4ped2<N2−2Np+2Nd4ped^2 < N^2 - 2Np + 2Nd \\

最后化简就得到攻击界是

4ped2<N2−2(p−d)N4ped^2 < N^2 - 2(p - d)N

此时kd\frac{k}{d}会是eN\frac{e}{N}的一个连分数收敛，枚举eN\frac{e}{N}的所有连分数收敛即可得到kk和dd（假设kk和dd互素）

继续化简·

以上的界看着不太美观，所以我选择继续进行化简

首先我会声称

2(p−d)≤23N2(p-d) \le \frac{2}{3}N

以下做简要证明：

首先因为dd是正整数，所以问题转化为证明

2(p−d)<2p≤2q3p2(p-d) < 2p \le \frac{2q}{3}p

也即需要证明q≥3q \ge 3，显然qq是一个大素数，所以一定成立

最后把2(p−d)≤23N2(p-d) \le \frac{2}{3}N代入，就可以得到界为

4ped2<13N3=N2−23N2<N2−2(p−d)N4ped^2 < \frac{1}{3}N^3 = N^2 - \frac{2}{3}N^2 < N^2 - 2(p - d)N

整理可得

ped2<112N2ped^2 < \frac{1}{12}N^2

PS：如果假设qq可以更大的话可以得到更大的系数，不过系数其实对界的影响不大，所以大概这样就算了

总结·

欢迎来纠错（无偿

整体和我用格推出来的界差不多，只不过用格算的话无法推出精确的系数，不过这里由于用了放缩法，所以系数112\frac{1}{12}其实也不太准确，只作参考

另外Boneh-Durfee的攻击其实也可推出一个与pp和ee相关的关系，不过Coppersmith的界推导实在是太麻烦了。。。