在SageMath中安装和使用G6K格筛算法。

目前最出名的G6K库应该是fplll-g6k，这个库只能用于C++或Python，但我个人更习惯用SageMath，考虑到SageMath可以兼容Python，所以打算装一波，并记录过程

安装过程主要参考fplll-g6k的Dockerfile，大概就是进入SageMath的shell，然后在里面编译和调用内置的Python进行安装

安装·

首先克隆仓库

1
2
git clone https://github.com/fplll/g6k.git
cd g6k

然后先check一下Sage内置的Python版本，输入sage -python，比如我的是

进入Sage的shell，打开里面的Python再check一下，看看是不是和上面的版本对应

1
sage -sh

我这里因为对python做了软链接，而没对python3做软链接，所以输python3出的Python版本和上面一样，实在不行可以在装的时候暂时把软链改一下，装完再改回去

版本和编译时间都一样，就可以执行下一步安装，在g6k/目录中（-j后面是编译的线程数，按实际情况更改）

1
2
3
python3 -m pip install -i https://pypi.tuna.tsinghua.edu.cn/simple -r requirements.txt
CFLAGS="-O2 -march=x86-64" CXXFLAGS="-O2 -march=x86-64" python3 setup.py build -j 8
python3 setup.py -q install

最后打开Sage，如无意外应该可以正常导g6k的库

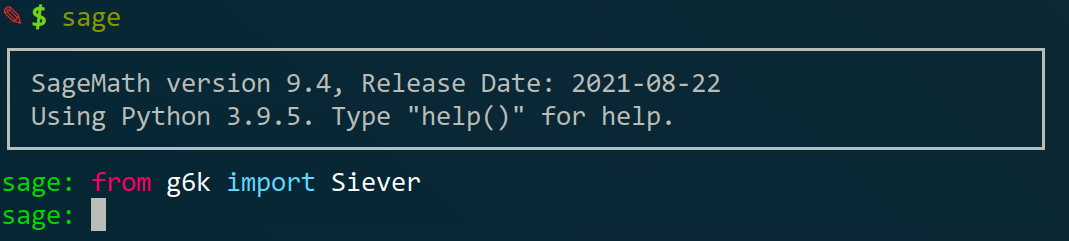
然后就装完了

使用·

前排提醒：G6K的用法我还没摸透，先记一些笔记，然后我也好像没有找到fplll-g6k的文档- -

首先Sage的矩阵可以直接传进fpylll的IntegerMatrix中，fpylll在SageMath中自带，不需要额外安装，然后再按照GitHub上的例子就可以

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#!/usr/bin/env sage
from fpylll import IntegerMatrix, LLL
from g6k import Siever

B = matrix(ZZ, n, ...)

A = IntegerMatrix(n, n)
A = A.from_matrix(B)
A = LLL.reduction(A)

g6k = Siever(A)
g6k.initialize_local(0, 0, n)
g6k(alg="gauss")
i, norm, coeffs = g6k.best_lifts()[0]
pritn(coeffs)

但实测筛出来的结果好像不太理想，原理不明

如果这里best_lifts()是空的话，也可以

1
db = list(g6k.itervalues())

然后在db里面找向量

封装一下的话大概就是

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#!/usr/bin/env sage
from fpylll import IntegerMatrix, LLL
from g6k import Siever

def g6k(B, best=True):
  n = B.nrows()
  assert n == B.ncols()
  A = IntegerMatrix(n, n)
  A = A.from_matrix(B)
  A = LLL.reduction(A)
  g6k = Siever(A)
  g6k.initialize_local(0, 0, n)
  g6k(alg="gauss")
  g6k()
  
  if best and g6k.best_lifts() != []:
    return matrix(ZZ, [x[2] for x in g6k.best_lifts()])

  db = list(g6k.itervalues())
  return matrix(ZZ, db)

但实测结果也不太理想，仓库里也没细说initialize_local的参数要怎么设置

先留个大坑（逃