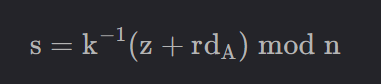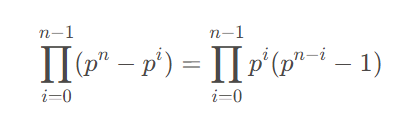babysign·

题目：https://paste.ubuntu.com/p/sKzFSKXNtQ/

很明显是ECDSA，找了下参考，主要是以下公式：

现在要求 $d_A$ ，所以转换一下：

$d_A = (sk-z)·r^{-1} \pmod n$

其中 $r$ 和 $s$ 就是输出的R和S， $k$ 是输出的nonce， $n$ 可以由ecdsa库获取， $z$ 是sha256(msg)，msg是b'welcome to ecdsa'，即只有 $d_A$ 是未知的，遂求之：

import hashlib
import libnum
import ecdsa

m = b'welcome to ecdsa'
z = int(hashlib.sha256(m).hexdigest(), 16)
r = 0x7b35712a50d463ac5acf7af1675b4b63ba0da23b6452023afddd58d4891ef6e5
s = 0xa452fc44cc36fa6964d1b4f47392ff0a91350cfd58f11a4645c084d56e387e5c
k = 57872441580840888721108499129165088876046881204464784483281653404168342111855
n = int(ecdsa.NIST256p.generator.order())

d = (s * k - z) * libnum.invmod(r, n) % n
flag = 'DASCTF{%s}' % libnum.n2s(int(d)).decode()
print(flag)

（感觉主要考代码阅读）

easyNTRU·

题目：https://paste.ubuntu.com/p/2KsjxkXVKn/

普通的NTRU（向量版本，不是Toy版本），关于NTRU的介绍这里就不累赘了，而且这题也不太需要知道NTRU的实现细节，实在要看的可以参考NTRU官方文档或[HPS14]。

首先，题目目标是恢复 $m$ 然后放sha3变成key再扔AES解密，而NTRU的解密需要私钥 $f$ 和 $g$ 。题目输出给了 $h$ ，根据密钥生成的 $h = f^{-1} · g\ in\ \mathbb{R}_q$ ，如果知道 $f$ 的话是可以通过 $g = f·h\ in\ \mathbb{R}_q$ 恢复 $g$ 的，所以即只需要恢复 $f$ 就好了（同理也可以只恢复 $g$ ）。

然后，题目的漏洞在于参数设置太小了， $f$ 的设置是f = T(d+1, d)，根据T函数的注释也可知道 $f$ 是 $N$ 维的向量，其中有 $d+1$ 个 $1$ 、 $d$ 个 $-1$ ，其余是 $0$ ，题目中的参数设置是N = 10、d = 3，可以算一下 $f$ 取值的可能性是：

$C_{N}^{d}·C_{N-d}^{d+1} = C_{10}^{3}·C_{7}^{4} = 4200$

非常小的数，爆破之（这里的爆破因为实在太小了，其实在while True:里一直取f = T(d+1, d)碰撞也是可以的）：

# sage
from Crypto.Hash import SHA3_256
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad

N = 10
p = 3
q = 512
d = 3

h = 39*x^9 + 60*x^8 + 349*x^7 + 268*x^6 + 144*x^5 + 469*x^4 + 449*x^3 + 165*x^2 + 248*x + 369
e = -144*x^9 - 200*x^8 - 8*x^7 + 248*x^6 + 85*x^5 + 102*x^4 + 167*x^3 + 30*x^2 - 203*x - 78
c = b'\xb9W\x8c\x8b\x0cG\xde\x7fl\xf7\x03\xbb9m\x0c\xc4L\xfe\xe9Q\xad\xfd\xda!\x1a\xea@}U\x9ay4\x8a\xe3y\xdf\xd5BV\xa7\x06\xf9\x08\x96="f\xc1\x1b\xd7\xdb\xc1j\x82F\x0b\x16\x06\xbcJMB\xc8\x80'

cypher = c

R.<x> = ZZ[]
def isT(f, d1, d2):
  fl = list(f)
  return fl.count(1)==d1 and fl.count(-1)==d2

def invertModPrime(f, p):
  Rp = R.change_ring(Integers(p)).quotient(x^N-1)
  return R(lift(1 / Rp(f)))

def convolution(f, g):
  return (f*g) % (x^N-1)

def liftMod(f, q):
  g = list(((f[i] + q//2) % q) - q//2 for i in range(N))
  return R(g)

def polyMod(f, q):
  g = [f[i]%q for i in range(N)]
  return R(g)

def decrypt(f, g):
  Fp = polyMod(invertModPrime(f, p), p)
  a = liftMod(convolution(f, R(e)), q)
  b = liftMod(convolution(Fp, a), p)
  m = b

  hobj = SHA3_256.new()
  hobj.update(bytes(str(m).encode('utf-8')))
  Key = hobj.digest()

  aes = AES.new(Key, AES.MODE_ECB)
  flag = aes.decrypt(cypher)
  try:
    flag = unpad(flag, 32)
    return flag
  except:
    return None

# 1 / (C_10^4)*(C_6^3)  =  1/4200
while True:
  fc = [0 for i in range(N)]
  for i in range(d+1):
    while True:
      pos = randrange(N)
      if fc[pos]==0:
        break
    fc[pos] = 1

  for i in range(d):
    while True:
      pos = randrange(N)
      if fc[pos]==0:
        break
    fc[pos] = -1

  f = R(fc)
  g = liftMod(convolution(f, R(h)), q)
  if not isT(g, d, d):
    continue

  flag = decrypt(f, g)
  if flag != None:
    print('f = %s' % f)
    print('g = %s' % g)
    print(flag)
    break

PS：其实用格的解法也是可以的，不过我懒（逃

NTRURSA·

题目：https://paste.ubuntu.com/p/VJcg2bc2Fn/

题目分两步，首先是普通的RSA，但是n = g * q ；然后是环S上的RSA，明文是h。所以解的时候是先解环S上的RSA解出h，然后用h解Toy NTRU解出g1，枚举rand拿g，最后解普通RSA。

首先环 $S$ 其实是个商环：

$S = \frac{\mathbb{Z}/p_2\mathbb{Z}[x]}{N(x)}$

感觉上可以近似地看成是个 $\rm{GF}(p_2^{\rm{degree}(N)})$ ，为什么要这样感觉呢，因为我要解c2 = m ^ e的RSA的话我需要知道 $S$ 的阶，而之前写 $\rm{GL}(n, \mathbb{F}_p)$ 群阶的时候引的一篇论文（好像）讲过 $\rm{GL}(n, \mathbb{F}_p)$ 和 $\rm{GF}(p^n)$ 是同构（？）的（大概就是 $\rm{GL}(n, \mathbb{F}_p)$ 的Jordan Form是在 $\rm{GF}(p^n)$ 上运算的），所以之前说的 $\rm{GL}(n, \mathbb{F}_p)$ 阶也可以放在这里用，但是这里的 $\rm{degree}(N)$ 有点大，用上次的代码的话需要挺长时间，所以可以用一个更大但是更容易算的：

测试了一下，可行，所以感觉是对的。然后剩下的就没啥好说的了，Toy NTRU的可以直接抄以前写过的代码：

# sage

e = 65537
p1 = 106472061241112922861460644342336453303928202010237284715354717630502168520267
c1 = 20920247107738496784071050239422540936224577122721266141057957551603705972966457203177812404896852110975768315464852962210648535130235298413611598658659777108920014929632531307409885868941842921815735008981335582297975794108016151210394446009890312043259167806981442425505200141283138318269058818777636637375101005540308736021976559495266332357714
p2 = 64621
c2 = 19921*x^174 + 49192*x^173 + 18894*x^172 + 61121*x^171 + 50271*x^170 + 11860*x^169 + 53128*x^168 + 38658*x^167 + 14191*x^166 + 9671*x^165 + 40879*x^164 + 15187*x^163 + 33523*x^162 + 62270*x^161 + 64211*x^160 + 54518*x^159 + 50446*x^158 + 2597*x^157 + 32216*x^156 + 10500*x^155 + 63276*x^154 + 27916*x^153 + 55316*x^152 + 30898*x^151 + 43706*x^150 + 5734*x^149 + 35616*x^148 + 14288*x^147 + 18282*x^146 + 22788*x^145 + 48188*x^144 + 34176*x^143 + 55952*x^142 + 9578*x^141 + 9177*x^140 + 22083*x^139 + 14586*x^138 + 9748*x^137 + 21118*x^136 + 155*x^135 + 64224*x^134 + 18193*x^133 + 33732*x^132 + 38135*x^131 + 51992*x^130 + 8203*x^129 + 8538*x^128 + 55203*x^127 + 5003*x^126 + 2009*x^125 + 45023*x^124 + 12311*x^123 + 21428*x^122 + 24110*x^121 + 43537*x^120 + 21885*x^119 + 50212*x^118 + 40445*x^117 + 17768*x^116 + 46616*x^115 + 4771*x^114 + 20903*x^113 + 47764*x^112 + 13056*x^111 + 50837*x^110 + 22313*x^109 + 39698*x^108 + 60377*x^107 + 59357*x^106 + 24051*x^105 + 5888*x^104 + 29414*x^103 + 31726*x^102 + 4906*x^101 + 23968*x^100 + 52360*x^99 + 58063*x^98 + 706*x^97 + 31420*x^96 + 62468*x^95 + 18557*x^94 + 1498*x^93 + 17590*x^92 + 62990*x^91 + 27200*x^90 + 7052*x^89 + 39117*x^88 + 46944*x^87 + 45535*x^86 + 28092*x^85 + 1981*x^84 + 4377*x^83 + 34419*x^82 + 33754*x^81 + 2640*x^80 + 44427*x^79 + 32179*x^78 + 57721*x^77 + 9444*x^76 + 49374*x^75 + 21288*x^74 + 44098*x^73 + 57744*x^72 + 63457*x^71 + 43300*x^70 + 1508*x^69 + 13775*x^68 + 23197*x^67 + 43070*x^66 + 20751*x^65 + 47479*x^64 + 18496*x^63 + 53392*x^62 + 10387*x^61 + 2317*x^60 + 57492*x^59 + 25441*x^58 + 52532*x^57 + 27150*x^56 + 33788*x^55 + 43371*x^54 + 30972*x^53 + 39583*x^52 + 36407*x^51 + 35564*x^50 + 44564*x^49 + 1505*x^48 + 47519*x^47 + 38695*x^46 + 43107*x^45 + 1676*x^44 + 42057*x^43 + 49879*x^42 + 29083*x^41 + 42241*x^40 + 8853*x^39 + 33546*x^38 + 48954*x^37 + 30352*x^36 + 62020*x^35 + 39864*x^34 + 9519*x^33 + 24828*x^32 + 34696*x^31 + 2387*x^30 + 27413*x^29 + 55829*x^28 + 40217*x^27 + 30205*x^26 + 42328*x^25 + 6210*x^24 + 52442*x^23 + 58495*x^22 + 2014*x^21 + 26452*x^20 + 33547*x^19 + 19840*x^18 + 5995*x^17 + 16850*x^16 + 37855*x^15 + 7221*x^14 + 32200*x^13 + 8121*x^12 + 23767*x^11 + 46563*x^10 + 51673*x^9 + 19372*x^8 + 4157*x^7 + 48421*x^6 + 41096*x^5 + 45735*x^4 + 53022*x^3 + 35475*x^2 + 47521*x + 27544
n = 31398174203566229210665534094126601315683074641013205440476552584312112883638278390105806127975406224783128340041129316782549009811196493319665336016690985557862367551545487842904828051293613836275987595871004601968935866634955528775536847402581734910742403788941725304146192149165731194199024154454952157531068881114411265538547462017207361362857
N = 25081*x^175 + 8744*x^174 + 9823*x^173 + 9037*x^172 + 6343*x^171 + 42205*x^170 + 28573*x^169 + 55714*x^168 + 17287*x^167 + 11229*x^166 + 42630*x^165 + 64363*x^164 + 50759*x^163 + 3368*x^162 + 20900*x^161 + 55947*x^160 + 7082*x^159 + 23171*x^158 + 48510*x^157 + 20013*x^156 + 16798*x^155 + 60438*x^154 + 58779*x^153 + 9289*x^152 + 10623*x^151 + 1085*x^150 + 23473*x^149 + 13795*x^148 + 2071*x^147 + 31515*x^146 + 42832*x^145 + 38152*x^144 + 37559*x^143 + 47653*x^142 + 37371*x^141 + 39128*x^140 + 48750*x^139 + 16638*x^138 + 60320*x^137 + 56224*x^136 + 41870*x^135 + 63961*x^134 + 47574*x^133 + 63954*x^132 + 9668*x^131 + 62360*x^130 + 15244*x^129 + 20599*x^128 + 28704*x^127 + 26857*x^126 + 34885*x^125 + 33107*x^124 + 17693*x^123 + 52753*x^122 + 60744*x^121 + 21305*x^120 + 63785*x^119 + 54400*x^118 + 17812*x^117 + 64549*x^116 + 20035*x^115 + 37567*x^114 + 38607*x^113 + 32783*x^112 + 24385*x^111 + 5387*x^110 + 5134*x^109 + 45893*x^108 + 58307*x^107 + 33821*x^106 + 54902*x^105 + 14236*x^104 + 58044*x^103 + 41257*x^102 + 46881*x^101 + 42834*x^100 + 1693*x^99 + 46058*x^98 + 15636*x^97 + 27111*x^96 + 3158*x^95 + 41012*x^94 + 26028*x^93 + 3576*x^92 + 37958*x^91 + 33273*x^90 + 60228*x^89 + 41229*x^88 + 11232*x^87 + 12635*x^86 + 17942*x^85 + 4*x^84 + 25397*x^83 + 63526*x^82 + 54872*x^81 + 40318*x^80 + 37498*x^79 + 52182*x^78 + 48817*x^77 + 10763*x^76 + 46542*x^75 + 36060*x^74 + 49972*x^73 + 63603*x^72 + 46506*x^71 + 44788*x^70 + 44905*x^69 + 46112*x^68 + 5297*x^67 + 26440*x^66 + 28470*x^65 + 15525*x^64 + 11566*x^63 + 15781*x^62 + 36098*x^61 + 44402*x^60 + 55331*x^59 + 61583*x^58 + 16406*x^57 + 59089*x^56 + 53161*x^55 + 43695*x^54 + 49580*x^53 + 62685*x^52 + 31447*x^51 + 26755*x^50 + 14810*x^49 + 3281*x^48 + 27371*x^47 + 53392*x^46 + 2648*x^45 + 10095*x^44 + 25977*x^43 + 22912*x^42 + 41278*x^41 + 33236*x^40 + 57792*x^39 + 7169*x^38 + 29250*x^37 + 16906*x^36 + 4436*x^35 + 2729*x^34 + 29736*x^33 + 19383*x^32 + 11921*x^31 + 26075*x^30 + 54616*x^29 + 739*x^28 + 38509*x^27 + 19118*x^26 + 20062*x^25 + 21280*x^24 + 12594*x^23 + 14974*x^22 + 27795*x^21 + 54107*x^20 + 1890*x^19 + 13410*x^18 + 5381*x^17 + 19500*x^16 + 47481*x^15 + 58488*x^14 + 26433*x^13 + 37803*x^12 + 60232*x^11 + 34772*x^10 + 1505*x^9 + 63760*x^8 + 20890*x^7 + 41533*x^6 + 16130*x^5 + 29769*x^4 + 49142*x^3 + 64184*x^2 + 55443*x + 45925


# ring RSA
R.<x> = PolynomialRing(GF(p2))
S.<x> = R.quotient(N)

nn = 175
p2n = p2^nn
phi2 = product([p2n-p2^i for i in range(nn)])
d2 = e.inverse_mod(phi2)
#print('d2 = %d' % d2)

m2 = S(c2)^d2
h = ''.join([str(x) for x in list(m2)])
h = int(str(int(h[::-1]))[::-1])  # remove 0s
print(h)

'''
m2 = 2*x^76 + 3*x^74 + 3*x^72 + 9*x^71 + 3*x^70 + 6*x^69 + 8*x^68 + 5*x^67 + 3*x^66 + 7*x^64 + x^63 + x^62 + 6*x^61 + 2*x^60 + 2*x^59 + 3*x^58 + 2*x^55 + 6*x^53 + 5*x^52 + 7*x^51 + 4*x^50 + 6*x^49 + 8*x^48 + 4*x^47 + 4*x^45 + 3*x^44 + x^43 + 4*x^42 + 9*x^41 + 8*x^40 + 4*x^39 + 4*x^38 + 2*x^37 + 6*x^36 + 2*x^35 + 3*x^32 + 4*x^30 + 5*x^29 + 7*x^28 + 3*x^27 + x^26 + 7*x^25 + x^24 + 3*x^23 + 2*x^22 + 5*x^21 + 3*x^20 + 8*x^19 + 4*x^18 + 4*x^17 + x^16 + 7*x^15 + 8*x^14 + 2*x^13 + 6*x^12 + 3*x^11 + x^9 + 9*x^8 + 2*x^7 + 4*x^6 + 2*x^5 + 2*x^3 + 5*x^2 + 8*x + 8
print(list(S(m2)))
h = 88520242910362871448352317137540300262448941340486475602003226117035863930302
'''

# toy NTRU
M = matrix([
    [1, h],
    [0, p1]
    ])
L = M.LLL()
b = vector(ZZ, L[0])
f1 = b[0]
g1 = b[1]

print(f1, g1)
assert f1.inverse_mod(p1)*g1 % p1 == h

# enumerate rand
from tqdm import tqdm
for rand in tqdm(range(2^20)):
  g = g1 ^^ rand
  if is_prime(g) and n % g == 0:
    q = n // g
    print('g = %d' % g)
    print('q = %d' % q)
    print('rand = %d' % rand)
    break

# normal RSA
phi1 = (g-1) * (q-1)
d1 = e.inverse_mod(phi1)
m1 = pow(c1, d1, n)

import libnum
flag = libnum.n2s(int(m1))
print(flag)

（感觉只是究极缝合，逃）

LWE?·

题目：https://paste.ubuntu.com/p/WDKQDRMkVs/

out：https://paste.ubuntu.com/p/dJTrNfQZSK/

感觉这题也不算难，但是全场最少解额

题目主要的地方是b = x*A+y*B+z*C+e，把这个式子用块矩阵重写一下就是：

$\begin{bmatrix} x & y & z\end{bmatrix} \begin{bmatrix} A \\ B \\ C\end{bmatrix} + e = b$

$\begin{bmatrix} A \\ B \\ C\end{bmatrix}$ 的行少于列，即转化为一个普通的LWE问题。套用这里的方法即解：

# sage

import re

m = 66
n = 200

with open('./out', 'r') as f:
  data = f.read().split('\n')
A = matrix(ZZ, [[int(x) for x in re.findall(r'-?\d+', x)] for x in data[1:m+1]])
B = matrix(ZZ, [[int(x) for x in re.findall(r'-?\d+', x)] for x in data[m+2:2*m+2]])
C = matrix(ZZ, [[int(x) for x in re.findall(r'-?\d+', x)] for x in data[2*m+3:3*m+3]])
b = vector(ZZ, [int(x) for x in re.findall(r'-?\d+', data[3*m+3])])

z = matrix(ZZ, [0 for _ in range(m)]).transpose()
beta = matrix(ZZ, [1])
T = block_matrix([[A, z], [B, z], [C, z], [matrix(b), beta]])

L = T.LLL()
e = L[0][:n]
print('e = %s' % e)

Mt = block_matrix([[A], [B], [C]])
xyz = Mt.solve_left(b-e)
secret = ''.join([chr(x) for x in xyz])
print(secret)

最后根据secret的提示组合出flag即可。

参考·

[HPS14] Hoffstein J, Pipher J, Silverman J H, et al. An introduction to mathematical cryptography[M]. New York: Springer, 2008.(https://www.springer.com/gp/book/9781441926746)