可证明安全学习笔记——Diffie-Hellman的被动攻击

如题

可证明安全是我研究生三年所学习的东西，感觉以后应该会很少搞这方面的东西了，总所周知，这东西一段时间不看的话就很容易会忘记，所以还是得做个笔记

Diffie-Hellman就是著名的DH密钥交换协议，用它做第一篇可证明安全学习笔记的原因有俩，一个是@Bintou在上周组会中刚好用DH做栗子给新人讲了可证明安全，另一个原因是，DH的协议比较简单，而且有一系列专门为它定制的难题，所以规约的过程也会相对简单

前置知识·

密钥交换·

所谓密钥交换，可以大概理解为：$P_i$和$P_j$两个参与方想要通信，但又不想他们的通信被别人窃听，所以会希望用一个密钥加密他们的信息，于是就会产生一个问题，密钥怎么协商呢

通常这个密钥我们想要的是对称密钥，原因是对称加解密的速度会比非对称加解密的速度快很多，而且如果用非对称加解密通信的话其实也并没有协商密钥的必要

一般来说，参与通信的双方的物理距离都很远，所以用线下协商密钥的方式并不现实，通常最容易会想到的另一种方法是，由某一方生成密钥，然后发送给另一方，但这显然是不行的，因为这个密钥可以被攻击者截获

所以，密钥交换协议要做就是，让通信双方协商出一个相同的密钥，而且这个密钥不能被第三方知道

关于密钥交换的更多内容建议自己翻一下wiki，这里就不展开了

协议流程·

首先DH协议通常运行在一个循环群$G$中，（$G$是一个通用的表达，为了方便理解，你可以直接令$G = \mathbb{Z}_p^*$，其中$p$是素数），令$G$的群阶为$|G| = q$，令$g$为$G$的生成元，即$G = <g>$

为了方便后面表述，这里设一个Gen函数，即$G, g, q \leftarrow \text{Gen()}$，来生成DH所使用的群

PS：一般$q$为素数，即$G$为素阶群

$$\begin{array}{|l|} \hline \begin{array}{lcl} \text{$P_i$} & \ \ \ \ \ \ \ \ \ \ \ \ \ & \text{$P_j$} \\ \begin{array}{l} \\ x \overset{\$}{\leftarrow} \mathbb{Z}_{q} \\ X = g^x \text{ (in $G$)} \end{array} & & \begin{array}{l} \\ y \overset{\$}{\leftarrow} \mathbb{Z}_{q} \\ Y = g^y \text{ (in $G$)} \end{array}\\ & \overset{X}{\longrightarrow} & \\ & \overset{Y}{\longleftarrow} & \\ \begin{array}{l} K_i = Y^x \text{ (in $G$)} \\ \end{array} & & \begin{array}{l} K_j = X^y \text{ (in $G$)} \\ \end{array}\\ \end{array} \\ \hline \end{array}$$

首先可以简单证明一下$P_i$和$P_j$在以上协议中生成了相同的密钥，即$K_i = K_j$：

$$K_i = Y^x = g^{yx} = g^{xy} = X^y = K_j \text{ (in $G$)}$$

然后就是证明其安全性，这篇文章的主要内容，留到后面说

可证明安全·

一个协议的安全性当然不是说“我认为它是安全的”，它就是安全的，而是需要严谨的证明

在可证明安全中有三个中重要的部件：安全定义、难题和规约：

• 安全定义：即定义一个协议符合什么条件才是安全的，通常在安全定义中会界定攻击者的攻击能力，即攻击者只能进行什么攻击，不能进行什么攻击
• 难题：顾名思义，就是一些被证明的或者公认的多项式时间内不可解决的问题，关于难题可以去复习一下计算理论
• 规约：比如说把问题$A$规约到问题$B$，大概的意思是，如果问题$B$被解了，那么问题$A$也可被解，关于规约也可以去复习一下计算理论

利用这三个部件，可证明安全的思路大概如下，其实是一个反证法：

• 首先构造一种规约，把某个难题规约到安全定义，详细点说即，如果存在一个符合我安全定义的攻击能力的攻击者，可以攻破我安全定义中设定的条件的话，那么就可以使用这个攻击者去解决这个难题
• 规约完成后，即是如果安全定义被攻击则难题被攻击，$\text{安全定义} \to \text{难题}$，如果把这个命题逆否一下，即$\neg\text{难题} \to \neg\text{安全定义}$，根据假设，难题在多项式时间内不可解，所以安全定义也在多项式时间内不可被攻破
• 另外，详细来说，在以上规约中，还需要一个模拟者$\text{S}$来模拟规约的过程，即假设存在一个攻击者$\text{A}$能够攻破我的安全定义，那么模拟者则需要通过调用$\text{A}$来解决难题

可以先把这个思路记住，然后在后面栗子中慢慢体会

PS：多嘴说一下，以上说的规约定义都是按照计算理论抄的，在别的论文或文章中会有一种像“方案的安全性可以规约到xxx问题”的说法，这里的“规约”比较像是这个方案基于xxx问题的意思，注意区分就好

安全难题·

马克一下后面会用到的一些难题，这些问题目前都只是假设，没有人能证明他是困难的，但目前（在$\mathbb{Z}_p^*$上）也没人能解

CDH假设·

计算性DH假设（Computational Diffie–Hellman assumption）

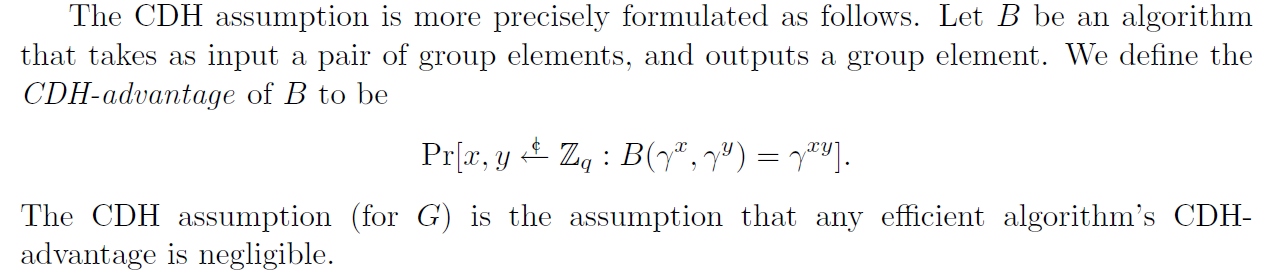
这个假设的大概意思是（可能会跟上图有点不一样）

令$G$为循环群，$g$为其生成元，$q$为其群阶，在$\mathbb{Z}_q$中均匀随机选择$x$和$y$，若存在攻击者$\text{A}$，在仅知道公开信息$(G, g, q)$和输入$(g^x, g^y)$的情况下，可以在多项式时间内计算出$g^{xy}$，则称攻击者$\text{A}$攻破了CDH难题

这个定义虽然没啥问题，但它只是定义了一个事件，我们很难把这个事件应用到证明中，所以一般会使用这个事件的概率，形式化地表示这个概率就是

$$\text{Pr} \begin{bmatrix} \begin{array}{ccc} \text{A}(g^x, g^y) = g^{xy} & \text{:} & x, y \overset{\$}{\leftarrow} \mathbb{Z}_{q} \end{array} \end{bmatrix}$$

准确地说，我们像知道的是攻击者的优势（Advantage），即攻击者$\text{A}$算中$g^{xy}$的概率比他睁着眼睛乱猜的概率大多少

由于攻击者乱猜的概率非常小（$1/q$），所以通常会忽略，即直接

$$\text{Adv}_\text{CDH}(\text{A}) := \text{Pr} \begin{bmatrix} \begin{array}{ccc} \text{A}(g^x, g^y) = g^{xy} & \text{:} & x, y \overset{\$}{\leftarrow} \mathbb{Z}_{q} \end{array} \end{bmatrix}$$

PS：个人认为准确点说应该是

$$\text{Adv}_\text{CDH}(\text{A}) := \begin{vmatrix} \text{Pr} \begin{bmatrix} \begin{array}{ccc} \text{A}(g^x, g^y) = g^{xy} & \text{:} & x, y \overset{\$}{\leftarrow} \mathbb{Z}_{q} \end{array} \end{bmatrix} - \frac{1}{q} \end{vmatrix}$$

不过人人都用上面哪个，就算了，反正写着更简单

最后如果对于所有多项式攻击者$\text{A}$，攻击CDH的优势都可忽略（Negligible），记作$\text{Adv}_\text{CDH}(\text{A}) \le \text{negl}$，则认为CDH问题不可被解决

反之如果存在一个多项式攻击者$\text{A}$，其攻击CDH的优势不可忽略，记作$\text{Adv}_\text{CDH}(\text{A}) > \text{negl}$，则CDH问题可被解决

CDH假设声称CDH问题不可被解决，则不存在优势不可忽略的多项式攻击者

DDH假设·

判定性DH假设（Decisional Diffie–Hellman assumption）

这个假设和上面的类似，但又不一样，大概意思是（可能会跟上图有点不一样）

令$G$为循环群，$g$为其生成元，$q$为其群阶，在$\mathbb{Z}_q$中均匀随机选择$x$、$y$和$z$，若存在攻击者$\text{A}$，在仅知道公开信息$(G, g, q)$和输入$(g^x, g^y, Z)$的情况下，可以分辨$Z = g^{xy}$还是$Z = g^z$，则称攻击者$\text{A}$攻破了DDH难题

类似地表达攻击者的优势（Game的定义）：

$$\text{Adv}_\text{DDH}(\text{A}) := \begin{vmatrix} \text{Pr} \begin{bmatrix} \begin{array}{ccc} \text{A}(g^x, g^y, Z) = b & \text{:} & \begin{array}{l} x, y, z \overset{\$}{\leftarrow} \mathbb{Z}_{q} \text{; } b \overset{\$}{\leftarrow} \{0, 1\} \\ Z = \left\{\begin{aligned} g^{xy} &, b = 0 \\ g^{z} &, b = 1 \end{aligned}\right. \end{array} \end{array} \end{bmatrix} - \frac{1}{2} \end{vmatrix}$$

这里的优势和CDH的会不太一样，因为攻击者$\text{A}$有$1/2$的概率猜$b$，这是个不可忽略的概率，所以需要减去

当然也可以用上面图的定义，即概率分布不可区分的定义

$$\text{Adv}_\text{DDH}(\text{A}) := \begin{vmatrix} \text{Pr} \begin{bmatrix} \begin{array}{ccc} \text{A}(g^x, g^y, g^{xy}) = 1 & \text{:} & x, y \overset{\$}{\leftarrow} \mathbb{Z}_{q} \end{array} \end{bmatrix} - \text{Pr} \begin{bmatrix} \begin{array}{ccc} \text{A}(g^x, g^y, g^{z}) = 1 & \text{:} & x, y, z \overset{\$}{\leftarrow} \mathbb{Z}_{q} \end{array} \end{bmatrix} \end{vmatrix}$$

但这个定义没有描述攻击游戏（Game），在规约的时候可能会有点麻烦，不过在Game Sequence的证明中会很好用，所以还是看具体证明中哪个好用来做选择吧

最后如果对于所有多项式攻击者$\text{A}$，攻击DDH的优势都可忽略（Negligible），记作$\text{Adv}_\text{DDH}(\text{A}) \le \text{negl}$，则认为DDH问题不可被解决

反之如果存在一个多项式攻击者$\text{A}$，其攻击DDH的优势不可忽略，记作$\text{Adv}_\text{DDH}(\text{A}) > \text{negl}$，则DDH问题可被解决

DDH假设声称DDH问题不可被解决，则不存在优势不可忽略的多项式攻击者

DDH规约到CDH·

到这里就可以先体验一波规约了，从上面定义不难看出，DDH可以规约到CDH，即如果CDH可解，则DDH可解，因为只要算出$g^{xy}$然后对比是否等于$Z$就可以了，下面来更严谨的证明

首先假设攻击者$\text{A}$可以解决CDH问题，以下构造模拟者$\text{S}$，通过调用攻击者$\text{A}$解决DDH问题（使用Game的定义），$\text{S}$的操作如下：

• 在接收到$(g^x, g^y, Z)$后，把$(g^x, g^y)$输入给攻击者$\text{A}$
• 接收到攻击者$\text{A}$输出的$Z_A$后，对比$Z_A$和$Z$是否相等，若相等则输出$0$，否则输出$1$

如果$\text{A}$成功解决CDH，则$Z_A = g^{xy}$，如果此时$Z_A = Z$，则$Z = g^{xy}$，即$b=0$，否则$Z \ne g^{xy}$，即只能$Z = g^z$，$b = 1$

所以如果$\text{A}$能成功攻击CDH的话，$\text{S}$也能成功攻击DDH

但其实$\text{A}$不是百分百成功攻击CDH的，所以通常会用两者的优势表示这个规约结果

$$\text{Adv}_\text{DDH}(\text{S}^\text{A}) \ge \text{Adv}_\text{CDH}(\text{A})$$

01-最简单的栗子（CDH）·

有了上面知识就可以看实际的栗子了，复习一下最开始的DH协议

$$\begin{array}{|l|} \hline \begin{array}{lcl} \mathrm{P_i} & \ \ \ \ \ \ \ \ \ \ \ \ \ & \mathrm{P_j} \\ \begin{array}{l} \\ x \overset{\$}{\leftarrow} \mathbb{Z}_{q} \\ X = g^x \text{ (in $G$)} \end{array} & & \begin{array}{l} \\ y \overset{\$}{\leftarrow} \mathbb{Z}_{q} \\ Y = g^y \text{ (in $G$)} \end{array}\\ & \overset{X}{\longrightarrow} & \\ & \overset{Y}{\longleftarrow} & \\ \begin{array}{l} K_i = Y^x \text{ (in $G$)} \\ \end{array} & & \begin{array}{l} K_j = X^y \text{ (in $G$)} \\ \end{array}\\ \end{array} \\ \hline \end{array}$$

首先要给出DH的安全定义，安全定义其实有很多种，只要别人认可，你也可以自己创一个安全定义

为了方便，我把DH协议的过程封装成一个DH函数（其中因为$K = K_i = K_j$，所以我就直接让$K = g^{xy}$了）

$$\begin{array}{|ll|} \hline & \text{DH$(G, g, q)$:} \\ \textcolor{lightgray}{01} & x, y \overset{\$}{\leftarrow} \mathbb{Z}_{q} \\ \textcolor{lightgray}{02} & X = g^x \text{ (in $G$)} \\ \textcolor{lightgray}{03} & Y = g^y \text{ (in $G$)} \\ \textcolor{lightgray}{04} & K = g^{xy} \text{ (in $G$)} \\ \textcolor{lightgray}{05} & \text{return $X, Y, K$} \\ \hline \end{array}$$

然后下面给一种DH中最简单的安全定义，以下定义攻击者$\text{A}$实施被动攻击DH的优势为：

$$\text{Adv}_\text{DH01}(\text{A}) := \text{Pr} \begin{bmatrix} \begin{array}{ccc} \text{A}(X, Y) = K & \text{:} & \begin{array}{l} G, g, q \leftarrow \text{Gen()} \\ X, Y, K \leftarrow \text{DH$(G, g, q)$} \end{array} \end{array} \end{bmatrix}$$

如果对于所有多项式的攻击者$\text{A}$，都有$\text{Adv}_\text{DH01}(\text{A}) \le \text{negl}$，则称DH协议安全

可以看出这个定义其实跟CDH的定义很像，所以会选择把它的安全性规约到CDH

假设存在攻击者$\text{A}$，能以$\text{Adv}_\text{DH01}(\text{A}) > \text{negl}$的优势攻破DH协议，以下构造模拟者$\text{S}$，通过调用$\text{A}$，以$\text{Adv}_\text{CDH}(\text{S}^\text{A}) > \text{negl}$的优势解决CDH问题，$\text{S}^\text{A}$的操作如下：

1. 在接收到CDH问题输入的$(g^x, g^y)$后，给$\text{A}$输入$(g^x, g^y)$

2. 接收到$\text{A}$输出的$K$后，输出$K$

显然，如果$\text{A}$可以成功攻破DH协议，则$K = g^{xy}$，恰好是CDH的解，所以有（因为至少知道$\text{A}$攻击成功的话$\text{S}$可以解难题，但不清楚$\text{S}$是否有其他途径解难题，所以是$\ge$）

$$\text{Adv}_\text{CDH}(\text{S}^\text{A}) \ge \text{Adv}_\text{DH01}(\text{A}) > \text{negl}$$

但根据CDH假设，$\text{Adv}_\text{CDH}(\text{S}^\text{A}) \le \text{negl}$，产生了矛盾，所以最开始的假设$\text{Adv}_\text{DH01}(\text{A}) > \text{negl}$不成立，即$\text{Adv}_\text{DH01}(\text{A}) \le \text{negl}$，DH协议安全

还算容易吧

02-猜比特（DDH）·

在以上定义中，需要攻击者恢复完整的Key，这其实是一个比较严格的要求，如果放宽对攻击者的要求的话，可以让攻击者只需猜Key的“一个比特”，那么如何定义这种猜“一个比特”，其实可以让攻击者某个输入是由DH算法生成的Key还是一个睁着眼睛乱选的Key

根据上面讨论，定义攻击者$\text{A}$猜中DH Key的优势为

$$\text{Adv}_\text{DH02}(\text{A}) := \begin{vmatrix} \text{Pr} \begin{bmatrix} \begin{array}{ccc} \text{A}(X, Y, K_b) = b & \text{:} & \begin{array}{l} G, g, q \leftarrow \text{Gen()} \\ X, Y, K_0 \leftarrow \text{DH$(G, g, q)$} \\ K_1 \overset{\$}{\leftarrow} G \text{; } b \overset{\$}{\leftarrow} \{0, 1\} \\ \end{array} \end{array} \end{bmatrix} - \frac{1}{2} \end{vmatrix}$$

注：因为攻击者即使乱猜也有$\frac{1}{2}$的概率猜中$b$，所以这里的优势需要减去这个$\frac{1}{2}$

如果对于所有多项式的攻击者$\text{A}$，都有$\text{Adv}_\text{DH02}(\text{A}) \le \text{negl}$，则称DH协议安全

可以看出这个定义其实跟DDH的定义很像，所以会选择把它的安全性规约到DDH

假设存在攻击者$\text{A}$，能以$\text{Adv}_\text{DH02}(\text{A}) > \text{negl}$的优势攻破DH协议，以下构造模拟者$\text{S}$，通过调用$\text{A}$，以$\text{Adv}_\text{DDH}(\text{S}^\text{A}) > \text{negl}$的优势解决DDH问题，$\text{S}^\text{A}$的操作如下：

1. 接收到DDH问题输入的$(g^x, g^y, Z)$后，把$(g^x, g^y, Z)$输入到$\text{A}$
2. 接收到$\text{A}$输出的$b$后，输出$b$

简单证明一下，如果DDH输入的$Z$是$g^{xy}$，则$Z$和安全定义的$K_0$同分布，如果$Z$是$g^z$，则$Z$和安全定义的$K_1$同分布，所以如果DDH问题里是$b=0$的情况，则$\text{S}$给$\text{A}$输入的是安全定义中$b=0$的情况，$\text{A}$应该以$\text{Adv}_\text{DH02}(\text{A})$的优势输出$b=0$，$b=1$的情况类似，略，所以

$$\text{Adv}_\text{DDH}(\text{S}^\text{A}) \ge \text{Adv}_\text{DH02}(\text{A}) > \text{negl}$$

但根据DDH假设，$\text{Adv}_\text{DDH}(\text{S}^\text{A}) \le \text{negl}$，产生了矛盾，所以最开始的假设$\text{Adv}_\text{DH02}(\text{A}) > \text{negl}$不成立，即$\text{Adv}_\text{DH02}(\text{A}) \le \text{negl}$，DH协议安全

由于这个规约也是比较直接，就不详细展开说了（应该还挺好懂吧，

03-多个Session（CDH）·

Session就是会话的意思，可以把DH协议中的一次密钥交换看作一个Session，即把上面协议图完整执行一遍后就是完成一个Session

在上面定义中，要求攻击者对于每一个Session都能算出其密钥，这对攻击者的要求有点高，因为在实际应用中，攻击者只需要猜中一个Session的Key就可能会产生严重的影响，所以需要一个新的定义，以放松对攻击者的要求

（注：由于一时间没找到相关定义，以下定义的一些部分是我自己编的）

首先定义一下Session如何产生，这里假设攻击者可以访问所有Session的Transcript（即DH协议中的$(X, Y)$），然后Session的数量固定，假设共有$n_s$个Session，以下定义一个Init函数，生成攻击游戏中所有Session的Transcript和Key

$$\begin{array}{|ll|} \hline & \text{Init$(n_s, G, g, q)$:} \\ \textcolor{lightgray}{01} & \mathcal{T} = [\ ] \\ \textcolor{lightgray}{02} & \mathcal{K} = [\ ] \\ \textcolor{lightgray}{04} & \text{for $i$ from $0$ to $n_s-1$:} \\ \textcolor{lightgray}{05} & \quad X_i, Y_i, K_i \leftarrow \text{DH$(G, g, q)$} \\ \textcolor{lightgray}{06} & \quad \mathcal{T}\text{.append($(X_i, Y_i)$)} \\ \textcolor{lightgray}{07} & \quad \mathcal{K}\text{.append($K_i$)} \\ \textcolor{lightgray}{08} & \text{return $\mathcal{T}, \mathcal{K}$} \\ \hline \end{array}$$

其中返回的$\mathcal{T}$就是所有Session的Transcript，$\mathcal{K}$就是所有Session的Key

于是以下定义攻击者$\text{A}$在多个Session中猜中一个Session Key的优势为：

$$\text{Adv}_\text{DH03}(\text{A}) := \text{Pr} \begin{bmatrix} \begin{array}{ccc} \begin{array}{l} \text{A}(\mathcal{T}) \to K \\ K \in \mathcal{K} \end{array} & \text{:} & \begin{array}{l} G, g, q \leftarrow \text{Gen()} \\ \mathcal{T}, \mathcal{K} \leftarrow \text{Init$(n_s, G, g, q)$} \end{array} \end{array} \end{bmatrix}$$

如果对于所有多项式的攻击者$\text{A}$，都有$\text{Adv}_\text{DH03}(\text{A}) \le \text{negl}$，则称DH协议安全

接下来是证明，大概思路和上一节的类似，安全性规约到CDH，假设存在攻击者$\text{A}$，能以$\text{Adv}_\text{DH03}(\text{A}) > \text{negl}$的优势攻破DH协议，以下构造模拟者$\text{S}$，通过调用$\text{A}$，以$\text{Adv}_\text{CDH}(\text{S}^\text{A}) > \text{negl}$的优势解决CDH问题

到这里有一个问题，就是$\text{S}$从CDH问题中只能拿到一对$(X_*, Y_*)$，而$\text{S}$调用$A$的时候需要给他$n_s$对不同的$(X_i, Y_i)$，所以下面$\text{S}$在调用$A$时需要自己生成$n_s - 1$对$(X_i, Y_i)$，然后再把CDH问题的$(X_*, Y_*)$嵌入其中，组成$n_s$对不同的$(X_i, Y_i)$作为$\text{A}$的输入

以下描述$\text{S}$的操作：

1. 在接收到CDH问题输入的$(g^x, g^y)$后，运行$\text{Init}(n_s-1)$获得$\mathcal{T}_\text{S}$和$\mathcal{K}_\text{S}$，把$(g^x, g^y)$嵌入到$\mathcal{T}_\text{S}$随机位置，然后把$\mathcal{T}_\text{S}$输入给$\text{A}$
2. 接收$\text{A}$的输出$K$，然后输出$K$

首先需要证明以上模拟中的$\mathcal{T}_\text{S}$和安全定义中的$\mathcal{T}$分布一致，不然攻击者$\text{A}$会在以上模拟中和安全定义中有不同的攻击优势，从而导致规约失败

明显，$\mathcal{T}_\text{S}$和$\mathcal{T}$只有嵌入的$(g^x, g^y)$分布（可能）不一样，在$\mathcal{T}$中由$\text{DH}(G, g, q)$抽样得出，在$\mathcal{T}_\text{S}$中则由CDH问题生成，由于CDH输出的$(g^x, g^y)$和$\text{DH}(G, g, q)$抽样的$(X, Y)$分布一致，所以易得$\mathcal{T}_\text{S}$和$\mathcal{T}$分布一致

而由于$\mathcal{T}_\text{S}$中的每个Transcript都分布一致而且相互独立，所以$\text{A}$只能在其中挑选一个$(X_i, Y_i)$去攻击出它的$K_i$，即$\text{A}$有$\frac{1}{n_s}$的概率挑中$(g^x, g^y)$然后攻击出对应的$K_*$

于是如果在以上模拟中$\text{A}$挑中了$(g^x, g^y)$而且成功攻击的话，$\text{S}$就可以成功攻击CDH，其中挑选中$(g^x, g^y)$的概率是$\frac{1}{n_s}$，随机挑选时成功攻击的优势是$\text{Adv}_\text{DH03}(\text{A})$，于是总结出$\text{S}^\text{A}$攻击CDH的优势为

$$\text{Adv}_\text{CDH}(\text{S}^\text{A}) \ge \frac{1}{n_s} \text{Adv}_\text{DH03}(\text{A}) > \text{negl}$$

注：关于可忽略量，一个多项式乘上一个可忽略量依然是可忽略量，反之，一个多项式乘上一个不可忽略量也依然是不可忽略量，这里$\frac{1}{n_s}$是多项式，所以在假设$\text{Adv}_\text{DH02}(\text{A})$为不可忽略量的前提下，$\text{Adv}_\text{CDH}(\text{S}^\text{A})$为不可忽略量

所以但根据CDH假设，$\text{Adv}_\text{CDH}(\text{S}^\text{A}) \le \text{negl}$，产生了矛盾，所以最开始的假设$\text{Adv}_\text{DH03}(\text{A}) > \text{negl}$不成立，即$\text{Adv}_\text{DH03}(\text{A}) \le \text{negl}$，DH协议安全

这里最后的优势表达和上一节的有点不同，多了个$\frac{1}{n_s}$，通常这种在$\text{A}$的优势前面多了个系数（通常这个系数小于$1$）的规约，都被称为不紧致（Non-tight）的规约，而像上一节的在$\text{A}$的优势前面没有系数的则称为紧致（Tight）规约

更紧致的规约？·

（注意：以下只是个人观点，不一定对，）

那么能不能把上面规约做紧致呢，目前来说如果没有额外假设的情况下，并不能在以上定义中基于CDH做到紧致，但好像能做得更紧致

观察一下上面的模拟，在接收到$\text{A}$的输出$K$后，如果$K$落在$\mathcal{K}_\text{S}$里的话，就可知道$\text{A}$对某个$(g^x, g^y)$以外的Transcript攻击成功，但$\text{S}$需要的是$(g^x, g^y)$对应的$K_*$，所以这个$K$肯定不是$\text{S}$想要的，所以若发现$K \in \mathcal{K}$，即可抛弃这个$K$，然后重新调用一次$\text{A}$进行攻击

于是，改进后的模拟者$\text{S}$的操作如下：

1. 接收CDH问题输入的$(g^x, g^y)$
2. 运行$\text{Init}(n_s-1)$获得$\mathcal{T}_\text{S}$和$\mathcal{K}_\text{S}$，把$(g^x, g^y)$嵌入到$\mathcal{T}_\text{S}$随机位置，然后把$\mathcal{T}_\text{S}$输入给$\text{A}$
3. 接收$\text{A}$的输出$K$，若$K \in \mathcal{K}_\text{S}$，则跳转到操作2，否则跳转到操作4
4. 输出$K$

首先分布一致的证明是一样的，这里就不重复了

然后这里有一个循环（Loop），所以需要证明模拟者$\text{S}$可以停机，即这个模拟者是多项式的，简单来说的话，这里至少$\text{A}$选中$(g^x, g^y)$的话是可以停机的，所以$\text{S}$停机的概率大于等于$\frac{1}{n_s}$，不是可忽略的概率，所以$\text{S}$依然是多项式的

接下来绑定$\text{S}$的优势，$\text{S}$的输出可以分为两种情况：$\text{A}$对任意一个Transcript攻击失败或者$\text{A}$对$(g^x, g^y)$的Transcript攻击成功

其中$\text{A}$对任意一个Transcript攻击失败的概率是$1 - \text{Adv}_\text{DH03}(\text{A})$，而$\text{A}$对$(g^x, g^y)$攻击成功的概率为$\frac{1}{n_s} \text{Adv}_\text{DH03}(\text{A})$，而$\text{S}$只有在$\text{A}$对$(g^x, g^y)$攻击成功时才能攻击成功，所以总结出$\text{S}$的优势为

$$\text{Adv}_\text{CDH}(\text{S}^\text{A}) \ge \frac{\frac{1}{n_s} \text{Adv}_\text{DH03}(\text{A})} {1 - \text{Adv}_\text{DH03}(\text{A}) + \frac{1}{n_s} \text{Adv}_\text{DH03}(\text{A})} = \frac{\text{Adv}_\text{DH03}(\text{A})} {n_s - (n_s-1) \text{Adv}_\text{DH03}(\text{A})} > \text{negl}$$

这个规约依然是不紧致的，因为令$n' = n_s - (n_s-1) \text{Adv}_\text{DH03}(\text{A})$的话，就是

$$\text{Adv}_\text{CDH}(\text{S}^\text{A}) \ge \frac{1}{n'} \text{Adv}_\text{DH03}(\text{A}) > \text{negl}$$

但是显然$n' \le n_s$，所以会比原来的紧致了一些

04-多Session猜比特（CDH）·

这一章有点问题，所以先删去

总结·

关于DH的被动攻击安全证明，大概就是以上这些

个人总结，未免有错，发现错误，请提Issue

然后，其实文章只是用了简单规约的技术，实际上用的比较多的还有Game Sequence的技巧，留个坑