正文·

首先验一下N1和N2，发现两个都不是素数，于是yafu分解一下，N2可以很快分解出来，然后发现有一个因子跟N1是相同的，于是得到：

p1 = 297342668339361548416629796745639177971
q1 = 92636417177965240871815246762704348071
assert p1*q1 == N1

p2 = 69857405335111415530599248077 
q2 = 92636417177965240871815246762704348071
assert p2*q2 == N2

根据[Jous21]里的Theorem 4.4，如果 $n=n_1*n_2$ 的话，就会有 $E_{A, B}(\mathbb{Z}_n)$ 同构于 $E_{A, B}(\mathbb{Z}_{n_1}) \bigoplus E_{A, B}(\mathbb{Z}_{n_2})$ ，而且如果点 $P$ 在 $E_{A, B}(\mathbb{Z}_n)$ 的话，点 $P_1 \equiv P\ (mod\ n_1)$ 和点 $P_2 \equiv P\ (mod\ n_2)$ 也会分别在 $E_{A, B}(\mathbb{Z}_{n_1})$ 和 $E_{A, B}(\mathbb{Z}_{n_2})$ 中：

所以给定 $Q = xP\ in\ E_{A, B}(\mathbb{Z}_n)$ 的话，可以先分别求出 $x_1 = QP^{-1}\ in\ E_{A, B}(\mathbb{Z}_{n_1})$ 和 $x_2 = QP^{-1}\ in\ E_{A, B}(\mathbb{Z}_{n_2})$ ，然后用 $x_1$ 和 $x_2$ 做个CRT就可以得到 $x$ 了（但要注意模数是用 $E_{A, B}(\mathbb{Z}_{n_i})$ 的阶，不是 $\mathbb{Z}_{n_i}$ 的阶）；也就是可以解出题中的d1和d2，然后解出flag；

经实验，q1和q2是相对容易解的，因为 $E_{A, B}(\mathbb{Z}_{q_1})$ 和 $E_{A, B}(\mathbb{Z}_{q_2})$ 的群阶可以分解成若干小的素数，用Pohlig–Hellman algorithm可以很快解出；p2分解出来的素数会大一点，但也算是可解的；Sage中的discrete_log好像就是直接用Pohlig–Hellman的，在椭圆曲线上的用法可以参考一下这个gist；

对于p1的话， $E_{A, B}(\mathbb{Z}_{p_1})$ 的群阶是个大素数，但是和p1是相等的，可以用Smart’s attack解，exp里copy了stackexchange里的一个回答的代码；于是最终脚本：

# Sage
import libnum

def SmartAttack(P,Q,p):
    E = P.curve()
    Eqp = EllipticCurve(Qp(p, 2), [ ZZ(t) + randint(0,p)*p for t in E.a_invariants() ])

    P_Qps = Eqp.lift_x(ZZ(P.xy()[0]), all=True)
    for P_Qp in P_Qps:
        if GF(p)(P_Qp.xy()[1]) == P.xy()[1]:
            break

    Q_Qps = Eqp.lift_x(ZZ(Q.xy()[0]), all=True)
    for Q_Qp in Q_Qps:
        if GF(p)(Q_Qp.xy()[1]) == Q.xy()[1]:
            break

    p_times_P = p*P_Qp
    p_times_Q = p*Q_Qp

    x_P,y_P = p_times_P.xy()
    x_Q,y_Q = p_times_Q.xy()

    phi_P = -(x_P/y_P)
    phi_Q = -(x_Q/y_Q)
    k = phi_Q/phi_P
    return ZZ(k)

N1 = 27544759469094453505371358768052861416297003882211878831861112512567899543941
A1 = 4208715803791813173086894172778966025419787767340027559010619240548499823390
B1 = 11846440123913040489420209031751160809904311707943252241515965930654415480691
P1x = 479750084250968709343887919962436485997147832319843477221083468203689368148
P1y = 15452861783577624143044213767588871736433639621547613407582902947429567101675

p1 = 297342668339361548416629796745639177971
q1 = 92636417177965240871815246762704348071
assert p1*q1 == N1

Gp1 = GF(p1)
Ep1 = EllipticCurve(Gp1, [0, 0, 0, A1, B1])
gp1 = Ep1([P1x, P1y])
yp1 = Ep1([
  14736970297054248276364510675718632926198693034158620007675880103924809577805,
  3447209262654420855289144268810543114387612255490962015335062266658385100211
])
#xp1 = discrete_log(yp1, gp1, gp1.order(), operation='+')
xp1 = SmartAttack(gp1, yp1, p1)
print('xp1 = %d' % xp1)
# xp1 = 244235039235837641751742977332387970532

Gq1 = GF(q1)
Eq1 = EllipticCurve(Gq1, [0, 0, 0, A1, B1])
gq1 = Eq1([P1x, P1y])
yq1 = Eq1([
  14736970297054248276364510675718632926198693034158620007675880103924809577805,
  3447209262654420855289144268810543114387612255490962015335062266658385100211
])
xq1 = discrete_log(yq1, gq1, gq1.order(), operation='+')
print('xq1 = %d' % xq1)
# xq1 = 379108844724449119014288379947197883

op1 = gp1.order()
oq1 = gq1.order()
x1 = crt([xp1, xq1], [op1, oq1])
flag1 = libnum.n2s(int(x1))
print(flag1)
# b'f4b9d58c-0f2b-4d7f'

# --- ---

N2 = 6471339743593595797696002766822660599108196938080465998531085409467
A2 = 3199218821393204771660095172457569312269694438403110131957204042314
B2 = 762889472027318213897694878260359911054972690369935049954326689904
P2x = 2557373437970770011124755960432555084678930336188254243278984381842
P2y = 4442763096366920105760404533052204677305995021662082361185473321644

p2 = 69857405335111415530599248077 
q2 = 92636417177965240871815246762704348071
assert p2*q2 == N2

Gp2 = GF(p2)
Ep2 = EllipticCurve(Gp2, [0, 0, 0, A2, B2])
gp2 = Ep2([P2x, P2y])
yp2 = Ep2([
  4834036103940457959470026215023033401071737087504569417466448644066,
  5511016821581393405975510064568222454318072088628361854656950557373
])
xp2 = discrete_log(yp2, gp2, gp2.order(), operation='+')
#xp = 64863796476861801236088764479
print('xp2 = %d' % xp2)

Gq2 = GF(q2)
Eq2 = EllipticCurve(Gq2, [0, 0, 0, A2, B2])
gq2 = Eq2([P2x, P2y])
yq2 = Eq2([
  4834036103940457959470026215023033401071737087504569417466448644066,
  5511016821581393405975510064568222454318072088628361854656950557373
])
xq2 = discrete_log(yq2, gq2, gq2.order(), operation='+')
#xq2 = 186120958764067501884848736278039519
print('xq2 = %d' % xq2)

op2 = gp2.order()
oq2 = gq2.order()
x2 = crt([xp2, xq2], [op2, oq2])
flag2 = libnum.n2s(int(x2))
print(flag2)
# b'-8c66-7ab0ae5e4621'

# --- ---
flag = flag1+flag2
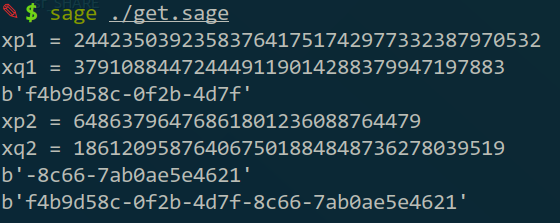
print(flag)
# b'f4b9d58c-0f2b-4d7f-8c66-7ab0ae5e4621'

参考·

[Jous21] Jousma W. Elliptic curves: an Introduction and Their Group Structure Over Z/NZ[D]. , 2021.

[Smart99] Smart N P. The discrete logarithm problem on elliptic curves of trace one[J]. Journal of cryptology, 1999, 12(3): 193-196.

[Muss06] Musson M. Attacking the Elliptec Curve Discrete Logarithm Problem[M]. Acadia University, 2006.