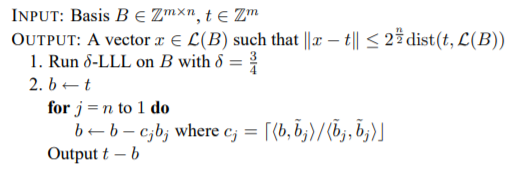（ 原文地址：https://0xffff.one/d/1064-yong-ge-jie-lwe-bi-ji ）

前言·

接上一篇继续讨论格密码的攻击，上一篇的几个问题几乎都是在解SVP(Shortest Vector Problem)问题，这次来讨论一个解CVP(Closest Vector Problem)问题的，即LWE(Learning With Errors)。

正文·

LWE·

虽然我个人认为，会接下去看的人应该都是知道LWE是啥的了（LWE不懂能看懂LWE的破解？），但还是简略讲一下LWE是个啥。

主要关注这样一个式子：

Ax+e=b (mod q)Ax+e=b\ (mod\ q)

其中A是个m*n的矩阵（公开）（好像m会比n大？如果n比m大的话就是一个长的x映射到一个短的b，就能有多个x映射到b导致不能解密了）；x是n*1的向量（明文）；e是误差，可以看成是每个元素都很小的m*1的向量（密钥）；b是m*1向量（密文）。运算都是在mod q下进行的，q是素数。详细点可以写成这样：

Am∗nxn∗1+em∗1=bm∗1 (mod q)A_{m*n}x_{n*1}+e_{m*1}=b_{m*1}\ (mod\ q)

在知道e的情况下，Ax=b−e (mod q)Ax=b-e\ (mod\ q)通过简单的高斯消元就可以解出x，即有私钥是容易解的。在没e的情况下，高斯消元会把误差e放大（好像是这么说的），所以只知道b会解不出x。

CVP·

CVP问题输入一个格L和一个通常不在格上的向量t，要求出在格上的离t“最近”的向量w。IMC上的定义：

通常来说，在维度小的情况下用LLL+Babai的方法可以解CVP问题，LLL主要用来找L的一组“很垂直”的基，Babai算法大概如下：

上面说的是L在RnR^{n}的情况，即L要是方阵，L不是方阵的话可以用Babai的"nearest plane algorithm"来解：

在Sage里，LLL可以直接用M.LLL()解，或者用free_module_integer里的IntegerLattice；CVP的话听说可以用free_module_integer的（且听说不是Babai的算法，试了一下，非常慢，放弃了，详细原因见下图），但还是手撸Babai的代码好一点。

解法·

解法参考了一下一篇 Aero CTF 2020 - Magic II 的wp，里面其实有挺详细的说明了（包括方程里矩阵的展开）。

首先现在问题是：

Ax+e=b (mod q)Ax+e=b\ (mod\ q)

知道A、b和q，e很小，求x，因为加了e，所以b大概率不会在格A中，但考虑到e很小，如果找到b在格A中最近的向量b‘，则有（其实b’是等于b-e ？）：

Ax=b′ (mod q)Ax=b'\ (mod\ q)

通过简单的高斯消元即可求出x。由于Babai的算法是不能在mod q的情况下解的，所以第一步是要先把mod q拆出来：

Ax+e=b (mod q)Ax+qImk=b−eAx+e=b\ (mod\ q) \\ Ax+qI_mk=b-e

其中，ImI_m是维度m的单位矩阵，k是拆mod q是的未知倍数（向量，m*1），即是把每一条aixi+kiq=bi−eia_ix_i+k_iq=b_i-e_i写成矩阵和向量的形式而已。由于多了个qImkqI_mk，所以要构造新的格，这也不难，根据上面式子马上有：

[ApIm][xk]=b−e\left[ \begin{array}{c|c} A & pI_m \end{array}\right] \begin{bmatrix} x \\ k \\ \end{bmatrix} = b-e

由于sage中的向量是横过来的（？？），所以左右做个转置：

[xk][ATpIm]=(b−e)T\left[ \begin{array}{c|c} x & k \end{array}\right] \begin{bmatrix} A^T \\ pI_m \\ \end{bmatrix} = (b-e)^{T}

当然也有另一种组合（实际尝试中会有上面那种不行，但下面的行的情况）：

[pImA][kx]=b−e[kx][pImAT]=(b−e)T\left[ \begin{array}{c|c} pI_m & A \end{array}\right] \begin{bmatrix} k \\ x \\ \end{bmatrix} = b-e \\ \left[ \begin{array}{c|c} k & x \end{array}\right] \begin{bmatrix} pI_m \\ A^T \\ \end{bmatrix} = (b-e)^{T}

例题·

以2020祥云杯的easy matrix为例，题目可以在这里找到。题目就是个LWE的加密，matrix是A、secret是x、offset 是e、result是b、prime是q。

按照上面的思路可以写出Sage脚本如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#!/usr/bin/env sage
from sage.modules.free_module_integer import IntegerLattice
import numpy as np

def Babai(B, t):
    # not square when using .LLL(), so use IntegerLattice ...
    B = IntegerLattice(B, lll_reduce=True).reduced_basis
    G = B.gram_schmidt()[0]
    b = t
    for i in reversed(range(B.ncols())):
        b -=  B[i] * ((b * G[i]) / (G[i] * G[i])).round()
    return t - b

mx = list(np.load('./matrix.npy'))
rt = list(np.load('./result.npy'))

A = matrix(ZZ, mx)
b = vector(ZZ, rt)
p = 2129
r = A.nrows()
c = A.ncols()

pIr = p*identity_matrix(r)
#M = block_matrix([[A.transpose()], [pIr]])  # [x, k]*[[A.t], [pIr]] = (b-e).t  (but not work ...
M = block_matrix([[pIr], [A.transpose()]])  # [k, x]*[[pIr], [A.t]] = (b-e).t   (this works ...
br = Babai(M, b)

print('e = %s' % (b-br))
R = IntegerModRing(p)
Ar = matrix(R, mx)
secret = Ar.solve_right(br)

m = ''.join(chr(x) for x in secret)
print('m = %s' % m)

在Babai里，本来以为可以直接用B.LLL()生成的基做的，但好像实际要用的是方阵的基，LLL()生成的基规模和B是一样的，无奈只能调用IntegerLattice的reduced_basis。

PS：写的时候参考了一下Lazzaro的代码，比较奇怪的是网上找easy matrix的wp发现代码几乎都是一样的，据说都是参考Nu1l的？震惊

总结·

CVP，LLL+Babai

参考·

  1. IMC
  2. Tel Aviv University, lattices_fall_2004, Lecture 3 CVP Algorithm
  3. 格密码 by Lazzaro
  4. 一篇 Aero CTF 2020 - Magic II 的wp
  5. Lattice-Based Cryptanalysis