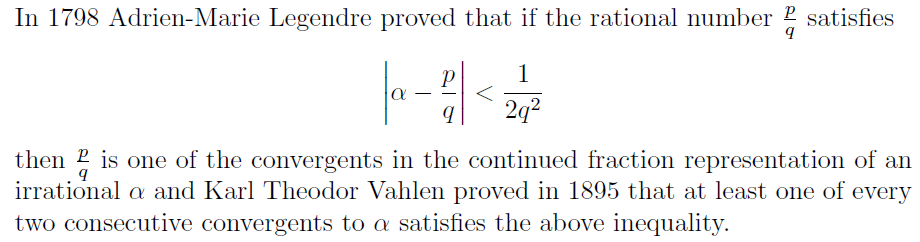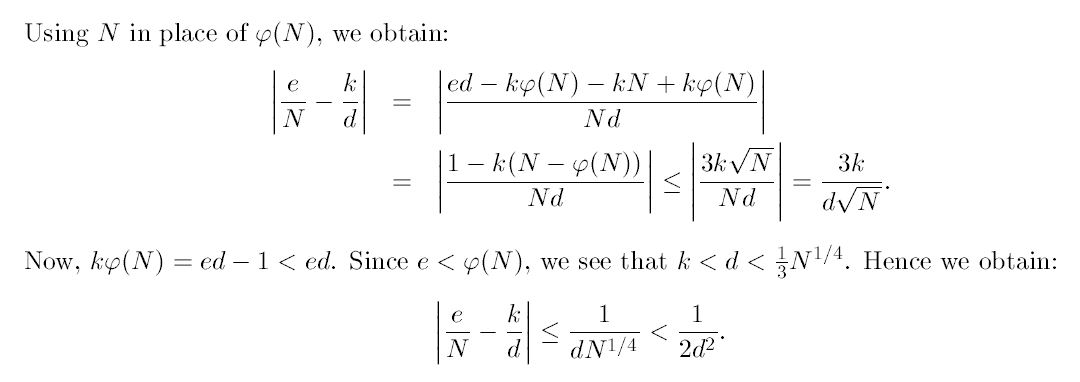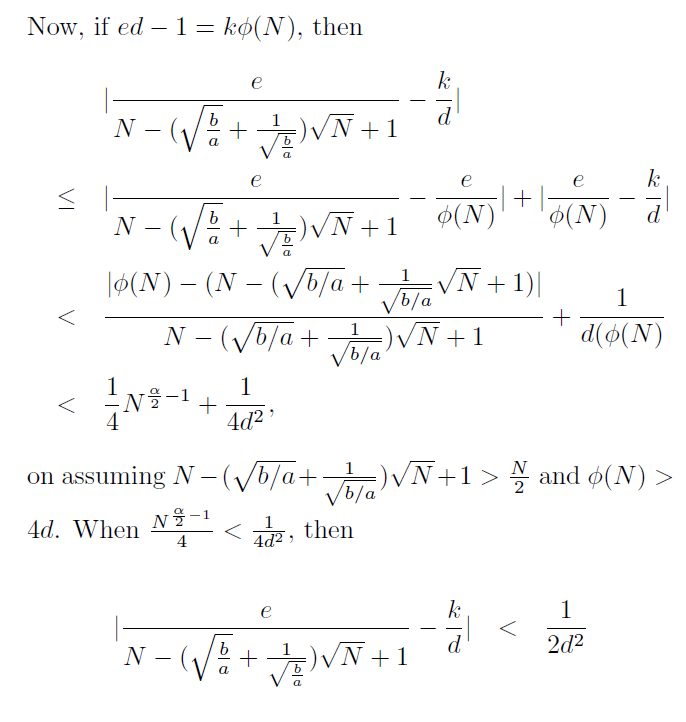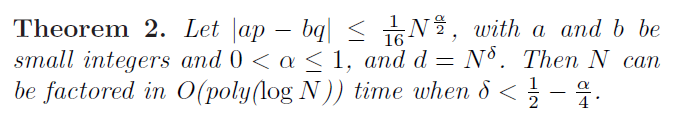Wiener's v.s Lattices —— Ax≡y(mod P)的方程解法笔记

（ 原文地址：https://0xffff.one/d/1062-wiener-s-v-s-lattices-ax-b-p-de-fang-cheng-xie-fa-bi-ji ）

前言·

填一下以前的坑，补习了一下Wiener’s attack和格密码攻击的内容，找到了其中一些共通之处，在这记个笔记（主要做题被暴打了- -

2021.10.16更新：

• 如无特殊说明文中假设$x,X,y,Y,s...$的是未知量，$a, A, b, B, P, ...$的是已知量；其中小写字母表示“小”的数，大写字母表示“大”的数；
• RSA多组密钥用同一个$d$；

2021.10.18更新：

• 连分数解方程和求某种格的最短向量的等同关系；
• Wiener’s attack revisited

正文·

About $Ax \equiv y \pmod P$·

这个问题也可等同于：$Ax+By=z$ ；

设有：

$$Ax≡y\ mod\ P$$

其中，$P$是素数~~（当然不是素数应该也可以？不过为了方便一些条件的讨论，比如求逆，还是假设素数）~~，$A$是大的数，$x$和$y$是小的数，这里说的大小关系是指（特殊情况下$x$或$y$还可以大一点，后面再说）：

$$A = \Theta(P)\\ x, y ≤ O(P^{1/2})$$

根据$Ax \equiv y \pmod P$，可以写成$Ax+kP=y$或$Ax-kP=y$，易得$k ≤ O(P^{1/2})$（$Ax=y+kP$的话，左右都是$≤O(P^{3/2})$的量级，$P$是$\Theta(P)$的，除一下就好了）

现在假设$A$和$P$已知，需要求$x$和$y$，那么根据以往的经验，一条方程中有三个未知数是不可解的，但现在有了大小关系的条件，就有两种方法可以解：

Wiener’s·

现有：

$$Ax-kP=y$$

左右同除$xP$：

$$\frac{A}{P}-\frac{k}{x}=\frac{y}{xP}$$

由于有$x, y ≤ O(p^{1/2})$，即有：

$$\frac{y}{xP} = \frac{1}{xP/y} ≤ \frac{1}{2*x^2}$$

于是就有了：

$$|\frac{A}{P}-\frac{k}{x}| ≤ \frac{1}{2*x^2}$$

就可以用连分数的方法（好像是Legendre’s theorem，其实Wiener攻击的核心就是连分数的逼近），用$A/P$逼近求出$k$和$x$（实际是$k/gcd(k,x)$和$x/gcd(k,x)$），进而也解出$y$。（到这步看不懂的话可以翻下面看Wiener’s扩展，逃

Lattices·

现有：

$$Ax+kP=y$$

如果增加一个恒等的式子：

$$x*1+k*0=x\\ xA+kP=y$$

就可以构造出：

$$(x, k)*\begin{bmatrix} 1 & A \\ 0 & P \\ \end{bmatrix} = (x, y)$$

令上面的东西记为：

$$v*M=w$$

还记得有$x, y ≤ O(P^{1/2})$，即可以算出：

$$\|w\| = (x^2+y^2)^{1/2} ≤ O(P^{1/2}) = \sqrt{2}P^{1/2} = \sqrt{2}det(M)^{1/2} ≈ \sigma(M)$$

所以$w$有很大概率为$M$里的最短向量，使用LLL算法reduce后可求出最短向量，即解出$w'=(x, y)$ 。（到这步看不懂的话可以翻下面看Latticces扩展，逃

更紧的界·

上面考虑的都是$x=\Theta (y)$的情况，如果 $x=o(y)$ 或者 $y=o(x)$ 呢。首先假设：

$$x = \Theta(P^\alpha) \\ y = \Theta(P^\beta)$$

根据上面构造出的$v*M=w$：

$$(x, k)*\begin{bmatrix} 1 & A \\ 0 & P \\ \end{bmatrix} = (x, y)$$

有：

$$w ≈ (P^\alpha, P^\beta)$$

推算一下的话可知道，$w$的长度其实是由“最大”的元素决定的，就是说假设$ \alpha>\beta$的话，有：

$$\|w\| ≈ \sqrt{2}\ P^\alpha$$

也就是如果对$w$和$M$的第二列同乘一个$c$，使得$a=\Theta(cb)$的话，$w$的长度不会有太大变化，但$det(M)$会明显变大，即$\sigma$会变大，推一下可知大概是$c \approx P^{\alpha-\beta}$。根据这个思路，可构造对角矩阵$D$：

$$D = \begin{bmatrix} 1 & 0 \\ 0 & P^{\alpha-\beta} \\ \end{bmatrix}$$

然后计算得到：

$$\|wD\| ≈ \sqrt{2}\ P^\alpha \\ \sigma(MD) ≈ \sqrt{2}\ P^{1/2+\frac{\alpha-\beta}{2}}$$

要能用Lattices的方法算的话，即：

$$\alpha < \frac{1}{2}+\frac{\alpha-\beta}{2} \\ \alpha+\beta < 1$$

也就是 $xy≤\Theta(P)$即可，也就是$x$和$y$一个小一点的话，另一个就可以大一点。$ \alpha<\beta$的情况也一样。

例题·

这里用[IMC]7.1节的"NTRU toy scheme"来作例子：

根据题目的信息可以推出：

$$fh≡g\ mod\ p\\ h = \Theta(q)\\ f, g ≤ O(q^{1/2})$$

Wiener’s做法：

#!/usr/bin/env sage
from Crypto.Util import number

BITS = 128
q = number.getPrime(BITS)
#f = number.getRandomRange(2, floor((q//2)^(1/2)))
#g = number.getRandomRange(2, floor((q//2)^(1/2)))
f = Integer(randint(2, floor((q//2)^(1/2))))
g = Integer(randint(2, floor((q//2)^(1/2))))
h = (f.inverse_mod(q)*g) % q

print('q = %s' % q)
print('f = %s' % f)
print('g = %s' % g)
print('h = %s' % h)

# debug
k = (f*h-g)//q
assert (f*h)%q == f*h-k*q
print((h/q-k/f) < 1/(2*f^2))
# end debug

f2 = f
g2 = g
N = 20000
fra = (h/q).n(N).exact_rational().continued_fraction()
for i in range(len(fra)):
    k = fra.numerator(i)
    f = fra.denominator(i)
    
    if f<=floor((q//2)^(1/2)) and f*h-k*q==(f*h)%q:
        g = f*h-k*q
        if g <= floor((q//2)^(1/2)):
            print(f2==f and g2==g, f, g)

在实践时搞出来的f和g有时会是原f和g的某个倍数（或整除），虽然还是符合$fh≡g\ mod\ p$

Lattices做法：

#!/usr/bin/env sage
from Crypto.Util import number

BITS = 128
q = number.getPrime(BITS)
#f = number.getRandomRange(2, floor((q//2)^(1/2)))
#g = number.getRandomRange(2, floor((q//2)^(1/2)))
f = Integer(randint(2, floor((q//2)^(1/2))))
g = Integer(randint(2, floor((q//2)^(1/2))))
h = (f.inverse_mod(q)*g) % q

print('q = %s' % q)
print('f = %s' % f)
print('g = %s' % g)
print('h = %s' % h)

M = matrix([
    [1, h],
    [0, q]
    ])

# debug
k = -(f*h-g)//q
assert (f*h)%q == f*h+k*q
a = vector(ZZ, [f, k])
b = vector(ZZ, [f, g])
assert a*M == b
lenB = (b*b)^(1/2)
detM = M.det()
print(lenB.n(10) <= ((detM)^(1/2)).n(10))
# end debug

f2 = f
g2 = g
L = M.LLL()
b = vector(ZZ, L[0])
f = abs(b[0])
g = abs(b[1])
print(f2==f and g2==g, f, g)

同样还是会有倍数的问题，但其实两个方法的倍数都很小，还是可以爆破出来（如果有条件爆破的话-

What about $A_ix_i \equiv Y \pmod P$ ？·

(前两天被吊打的hws) 如果是$Y$是未知大数的情况怎么样呢，即：

$$A_ix_i \equiv Y \pmod P \\ A_i, Y = \Theta(P)\\ x_i ≤ O(P^{\alpha_i})$$

知道$A_i$和$P$，求$x_i$和$Y_i$。如果有多组这样的式子的话是可以转化成$Ax \equiv y \pmod P$的情况的。

先来看一下$x_iY=A_i \pmod P$的情况：

$$x_1Y \equiv A_1 \pmod P \\ x_2Y \equiv A_2 \pmod P$$

可以推出（不排版了，能看懂就好-）：

$$x' = (A_1Y^{-1} \equiv x_1 \pmod P)\ \ \ \ \ \ ≤ O(P^{\alpha_1}) \\ y' = (A_2Y^{-1} \equiv x_2 \pmod P)\ \ \ \ \ \ ≤ O(P^{\alpha_2}) \\ A' = ({A_1}^{-1}A_2 \equiv {x_1}^{-1}x_2 \pmod P)\ \ \ \ \ \ =\Theta(P)$$

即可消去未知大数$Y$：

$$A'x' \equiv y' \pmod P$$

再来看回$A_ix_i \equiv Y \pmod P$，其实只要稍微转化成：

$$x_iY^{-1} \equiv A_i^{-1} \pmod P$$

就是上面的情况。

What about $A_ix_i \equiv Y_i \pmod P$ ？·

按照上面的经验，要解这东西，就要消去$Y_i$，但我目前没有找到消去的方法，所以暂时不会解（？？？

What about $\sum_{i=1}^{n} A_ix_i \equiv y \pmod P$·

这个问题也可等同于： $\sum_{i=1}^{n} A_ix_i = y$ ；

$$\sum_{i=1}^{n} A_ix_i \equiv y \pmod P \\ \sum_{i=1}^{n} A_ix_i + kP = y \\ \ \\ (x_1, x_2, ..., x_n, k) \begin{pmatrix} 1 & 0 & \cdots & 0 & A_1 \\ 0 & 1 & \cdots & 0 & A_2 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & A_n \\ 0 & 0 & \cdots & 0 & P \\ \end{pmatrix} \\ = (x_1, x_2, ..., x_n, y)\\ \ \\$$

记上式为$vM=w$；记$x_{max} = max(x_i)$，有：

$$\sigma(M) ≈ \sqrt{n+1}\ P^{1/(n+1)} \\ \|w\| ≈ \sqrt{n+1}\ x_{max}$$

所以只要有 $x_{max}≤O(P^{1/(n+1)})$ 就可解 $x_i$ ；这里同样可以用乘上一个对角阵$D$的方法尽量把$\sigma(M)$放大，跟“更紧的界”里说的一样所以略了（后面大部分方法都是适用的）。

PS：这个矩阵跟解背包密码（Knapsacks）的那个矩阵有点像，但又不完全像，因为两个问题其实就有点像，但又不完全像（逃

What about $\sum_{i=1}^{n} A_ix_i \equiv B \pmod P$·

这个问题也可等同于：$\sum_{i=1}^{n} A_ix_i = B$ ；

如果现在等式右边是大数$B$，而且$B$已知的话，就是背包密码（Knapsacks）的解法了：

$$\sum_{i=1}^{n} A_ix_i \equiv B \pmod P \\ \sum_{i=1}^{n} A_ix_i + kP - B = 0 \\ \ \\ (x_1, x_2, ..., x_n, k， -1) \begin{pmatrix} 1 & 0 & 0 & \cdots & 0 & 0 & A_1 \\ 0 & 1 & 0 & \cdots & 0 & 0 & A_2 \\ 0 & 0 & 1 & \cdots & 0 & 0 & A_3 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & 1 & 0 & A_n \\ 0 & 0 & 0 & \cdots & 0 & 1 & P \\ 1 & 1 & 1 & \cdots & 1 & 1 & B \\ \end{pmatrix} \\ = (x_1-1, x_2-1, ..., x_n-1, k-1, 0)\\ \ \\$$

记上式为$vM=w$；记$x_{max} = max(x_i)$，有：

$$\sigma(M) ≈ \sqrt{n+2}\ P^{1/(n+2)} \\ \|w\| ≈ \sqrt{n+2}\ x_{max}$$

注意到这里其实$w$的最后一个元素是$0$，所以如果$M$的最后一列和$w$的最后一个元素同乘一个超大的$C$的话（即$M$和$w$同乘一个对角阵$D$，$D$的对角线上的最右下一个是$C$，其他是$1$），$det(M)$会变大，而$w$则不变，可以得到：

$$\sigma(MD) ≈ \sqrt{n+2}\ (CP)^{1/(n+2)} \\ \|wD\| ≈ \sqrt{n+2}\ x_{max}$$

所以如果$C$足够大的话，就会有$\|wD\| ≤ \sigma(MD)$，即可解 $x_i$（理论上

What about $A_ix_i \equiv y_i \pmod {(P+s)}$·

现在假设模数未知，但可以拆成$(P+s)$，$P$已知，$s$未知但很“小”：

$$A_i = \Theta(P) \\ x_i ≤ O(P^\alpha) \\ y_i ≤ O(P^\beta) \\ s ≤ O(P^\gamma)$$

比如RSA中，$\phi(N)$并不知道，但会知道 $N=\phi(N)+(1-(p+q))$，用类似 扩展维纳攻击[HS99] 的方法可以用$(P+s)$代替原来的模数，然后用格的方法做，但需要的$x$和$y$要更小。（其实这部分就是在讲扩展维纳攻击）

假设现在是有两组的情况：

$$A_1x_1 \equiv y_1 \pmod {(P+s)} \\ A_2x_2 \equiv y_2 \pmod {(P+s)}$$

拆开：

$$A_1x_1+k_1P = y_1-k_1s \ \ \ \ \ \ \ \ ① \\ A_2x_2+k_2P = y_2-k_2s \ \ \ \ \ \ \ \ ②$$

可以看到①和②两个方程的未知数很不一样，即很难构造像之前的线性方程，但是看一下①*②的式子：

$$(A_1x_1+k_1P)(A_2x_2+k_2P) = A_1A_2x_1x_2+A_1Px_1k_2+A_2Px_2k_1+P^2k_1k_2$$

通过$①*k_2$和$②*k_1$的方式，构造出来的未知数不会比①*②中的多，于是就可以构造出下面四条方程（构造时尽量弄成上三角的矩阵）：

1. 恒等式引入$k_1k_2$

$$k_1k_2 = k_1k_2$$

2. $①*k_2$

$$A_1x_1k_2+k_1Pk_2 = (y_1-k_1s)k_2$$

3. $①*k_2-②*k_1$

$$A_1x_1k_2-A_2x_2k_1 = (y_1k_2-k_1sk_2)-(y_2k_1-k_2sk_1) = y_1k_2-y_2k_1$$

4. ①*②

$$A_1A_2x_1x_2+A_1Px_1k_2+A_2Px_2k_1+P^2k_1k_2 = (y_1-k_1s)(y_2-k_2s)$$

重点关注第3条，很巧妙地把右边的$sk_1k_2$消去了，使得$\alpha$或$\beta$可以更大一点，这也是扩展维纳攻击$d$的大小比普通维纳攻击d的大小大一点的原因（吗？

于是就有：

$$(k_1k_2, x_1k_2, x_2k_1, x_1x_2) \begin{pmatrix} 1 & P & 0 & P^2 \\ 0 & A_1 & A_1 & A_1P \\ 0 & 0 & -A_2 & A_2P \\ 0 & 0 & 0 & A_1A_2 \end{pmatrix} \\ =(k_1k_2, (y_1-k_1s)k_2, y_1k_2-y_2k_1, (y_1-k_1s)(y_2-k_2s))$$

记作$vM=w$，跟之前同样的方法构造$D$把$w$弄齐次（这里先假设 $\alpha+\gamma \ge \beta$，即$w$最大元素约为$P^{2\alpha+2\gamma}$）：

$$w ≈ (P^{2\alpha}, P^{2\alpha+\gamma}, P^{\alpha+\beta}, P^{2\alpha+2\gamma}) \\ D = \begin{pmatrix} P^{2\gamma} & 0 & 0 & 0 \\ 0 & P^{\gamma} & 0 & 0 \\ 0 & 0 & P^{\alpha-\beta+2\gamma} & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \\$$

可以计算：

$$\sigma(MD) ≈ 2P^{1+\frac{5\gamma+\alpha-\beta}{4}} \\ \|wD\| ≈ 2P^{2\alpha+2\gamma}$$

要最短向量为$w$即：

$$\|wD\| ≤ \sigma(MD) \\ 2\alpha+2\gamma ≤ 1+\frac{5\gamma+\alpha-\beta}{4} \\ 7\alpha+\beta+3\gamma ≤ 4$$

在扩展维纳攻击中是$\beta=0$，$\gamma=1/2$，所以算出$\alpha≤5/14$。

另外，在假设 $\alpha+\gamma<\beta$ 的情况下，推出：$\alpha+\beta ≤ 1$，即和之前一样 。

可以看出上面的情况$\alpha$和$\beta$的系数和都是右边的两倍，而且还引入了$\gamma$，所以在$\alpha≈\beta$的情况下，$\alpha$和$\beta$都需要更小（不会比已知$(P+s)$的解法更优）。

What about $a_iX \equiv y_i \pmod {(P_i+s_i)}$·

这个问题也可等同于：$a_iX + B_iy_i = z_i$ ；（其实好像和上一个也有点像？）

RSA多组密钥用同一个$d$的情况，只不过那是$e_id \equiv 1 \pmod {n_i}$；现知道$a_i、P_i$，其他未知，有：

$$X,P_i = \Theta(P) \\ a_i \le O(P^\alpha) \\ y_i \le O(P^\beta) \\ s_i \le O(P^\gamma) \\ \alpha, \beta, \gamma < 1 \\ a_iX \equiv y_i \pmod {(P_i+s_i)} \\ a_iX +k_iP_i = y_i - k_is_i \\ k_i \approx a_i \le O(P^\alpha)$$

即可构造：

$$(X, k_1, k_2, ..., k_n) \begin{pmatrix} 1 & a_1 & a_2 & \cdots & a_{n-1} & a_n \\ 0 & P_1 & 0 & \cdots & 0 & 0 \\ 0 & 0 & P_2 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & P_{n-1} & 0 \\ 0 & 0 & 0 & \cdots & 0 & P_n \\ \end{pmatrix} \\ = (X, y_1-k_1s_1, y_2-k_2s_2, ..., y_n-k_ns_n)$$

记上式为$vM=w$；先假设$\beta \le \alpha+\gamma \le1$，得：

$$w \approx (P, P^{\alpha+\gamma}, P^{\alpha+\gamma}, ..., P^{\alpha+\gamma}) \\ D = \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & P^{1-(\alpha+\gamma)} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & P^{1-(\alpha+\gamma)} \end{pmatrix} \\$$

计算出：

$$\sigma(MD) ≈ \sqrt{n+1} P^{\frac{n}{n+1}+\frac{n(1-(\alpha+\gamma))}{n+1}} \\ \|wD\| ≈ \sqrt{n+1} P$$

要最短向量为$w$即要符合：

$$1 \le \frac{n}{n+1}+\frac{n(1-(\alpha+\gamma))}{n+1} = \frac{n}{n+1}(2-(\alpha+\gamma))$$

即：

$$1/n \le 1-(\alpha+\gamma)$$

• 若$\alpha+\gamma \le \beta \le1$，同样的方法可算出需符合：

$$1/n \le 1-\beta$$

• 若$\beta \le 1 \le \alpha+\gamma$，需符合：

  $$\alpha+\gamma \le 1-1/n$$

  因为有$1 \le \alpha+\gamma$，即无解。

What about $A_i=xy_i+z_i$·

其实这是ACD问题，参考[GGM16]，和21wmctf的easylsb。

现有（把论文的符号换了一下。。。）：

$$x = \Theta(2^\alpha)\\ y_i = \Theta(2^\beta)\\ z_i = \Theta(2^\rho)\\ \rho<\alpha\\ \rho<\beta\\ ↓\\ A_i = \Theta(2^{\alpha+\beta})$$

其中[GGM16]第三章中提到一个技巧，$A$是很大的，但是$A_iy_0-A_0y_i$可以减少规模：

$$A_iy_0-A_0y_i = (xy_i+z_i)y_0-(xy_0+z_0)y_i = y_0z_i-y_iz_0\\ 2^{\alpha+2\beta} → 2^{\beta+\rho}$$

于是构造：

$$(y_0, y_1, ..., y_n) \begin{pmatrix} R & A_1 & A_2 & \cdots & A_n \\ 0 & -A_0 & 0 & \cdots & 0 \\ 0 & 0 & -A_0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & -A_0 \\ \end{pmatrix} _{(n+1)*(n+1)} \\ =(y_0R, A_1y_0-A_0y_1, ..., A_ny_0-A_0y_n)\\ =(y_0R, y_0z_1-y_1z_0, ..., y_0z_n-y_nz_0)$$

记上式为$vM=w$，其中设$R=2^\rho$，这里的$R$的作用其实是上面“更紧的界”里说的要把$w$配齐次。可以算出：

$\sigma(M) ≈ \sqrt{n+1}\ 2^{(n(\alpha+\beta)+\rho)/(n+1)} \\ \|w\| ≈ \sqrt{n+1}\ 2^{\beta+\rho}$

要能用格解，则：

$$\beta+\rho \le (n(\alpha+\beta)+\rho)/(n+1)\\ \beta \le n(\alpha-rho)$$

在“easylsb”中是$n=4, \beta=\alpha=512, \rho=368$，$512 \le 4(512-368) = 4*144=576$

(PS：瞎写的，待验证)

Wiener’s 扩展·

现在说的Wiener’s attack指Wiener在[Wiener90]提出的针对RSA的攻击，但其实更多时候说的是他用到的方法，即Legendre’s theorem（其实这里说的也是，也许只是Wiener当时的攻击比较出名？）：

就是说如果能找到$\alpha$符合上面的关系的话，那$p/q$就是$\alpha$那堆连分数里的其中一个，$\alpha$是知道的，所以$\alpha$的连分数可以求出来，$p$和$q$就是$\alpha$某一个连分数的分子和分母（当然也可能会是某个倍数）。

Wiener’s attack说的是在RSA中，当$d$很小时（$d<\frac{1}{3}N^{1/4}$），可以通过连分数的方法解出$d$。先来看看RSA的密钥生成，$ed ≡ 1 \ mod\ \phi(N)$，$e$是大的，$d$是小的，$1$是小的，刚好符合上面说的方程大小关系，于是可以：

$$ed ≡ 1 \ mod\ \phi(N) \\ ed-k\phi(N) = 1 \\ |\frac{e}{\phi(N)}-\frac{k}{d}| = \frac{1}{d\phi(N)} < \frac{1}{2d^2}$$

好像可以解，但问题在于$\phi(N)$是不知道的，于是需要一些“近似替换”的方法。由于$p, q ≈ O(N^{1/2})$，所以：

$$\phi(N) = (p-1)(q-1) = N-p-q+1 ≈ N$$

于是就可以用N来近似$\phi(N)$，由于$N$是知道的就可以求$k$和$d$，但需要一个证明[Bon99 Th.2]：

然后就可以愉快地用$e$和$N$计算$k$和$d$了。

Wiener’s attack是1990提出来的东西了，所以后来也有了很多改进的版本，用其他的东西近似替换$\phi(N)$，而不是用$N$，比如

上面那个是[OP12]里的一个定理：

2020的湖湘杯的crypto4就照搬了这个定理（网上找不到writeup，最近拿出来鞭尸x）（原题忘了，只剩个图）

wp：

# sage
from gmpy2 import iroot
import libnum

n = 45644374572906696918751526371540317432552767574531146725947197073091284249824311652929876880761183040024642912502639494246699284890420348711755152172125722304276541146638287085067604879135037538874624825231963426170448359129554061563687341132377272549120305441316002675552272436786866637426883885955669
e = 41481590714555165448395765336905824124002290841668481529563451625379681482568747653473952507567741287320305714776744069287119560788311144707988486438017581271859974139810844158857833808782692691546769253874942787868189158458052798618813933937987400708792117152522747046613196233766095230599127585735387
c = 25790054143492912038696919999059363251926853333642241274795090550534183356849875749287324824373062006504574906179764092648413976672912657535347328280694667704633525599132436478280986985933339098397197660180557793681265237430974006426519650760258181942099887311223904706872308373765682748061276137390494
i = 11
j = 2

X = 1000
rho = 11/2
sn = (sqrt(n)).n(X)
sr = (sqrt(rho)).n(X)
sij = (sqrt(i*j)).n(X)

left = e/(n-((i+j)/sqrt(i*j))*sqrt(n)+1)
fra = (left.n(X).exact_rational()).continued_fraction()
print(len(fra))

for i in range(1, len(fra)):
    k = fra.numerator(i)
    d = fra.denominator(i)
    if (e*d-1)%k==0:
        print(k, d)
        x = var('x')
        sol = solve([x^2-(n+1-(e*d-1)/k)*x+n==0], x)
        p = sol[0].right()
        q = sol[1].right()
        if p.is_integer() and q.is_integer():
            print('d = %s' % d)
            print('p = %s' % p)
            print('q = %s' % q)
            print(libnum.n2s(int(pow(c, d, n))))
            break
    #print(i)

# DASCTF{d10a6523ab3c9b26238b523f1a9e3c73}

Lattices 扩展·

格（Lattices）的话可以看成是一个向量空间里的一堆点，就是一组基通过“整数”的线性组合“张成”的空间（具体可以看[IMC]的7.4，那里会说得更详细）。

这里主要说一下用格解方程的方法和原理。主要用到一个叫Gaussian expected shortest length的东西：

就是说，在格$L$中的最短非零向量的长度大概有$\sigma(L)$那么长，如果可以构造出整数向量$v$、$w$和格$L$（其中$v$、$w$未知，$L$已知），使得：

$$vL = w \\ ||B|| ≤ \sigma(L)$$

的话，$w$就大概率是$L$的最短向量（第一个式子说明向量$w$在格$L$中，第二个式子说明$w$大概率是$L$的最短向量），通过找$L$的最短向量可解出$w$，通过$w*L^{-1}$可解$v$。在$L$的维度不大的情况下，用LLL算法可以找到L的最短向量（Sage中可以直接调用，详细原理可以看[IMC]的7.13），LLL算法主要用于把“垂直程度低”的格“reduce”成“垂直程度高”的格，而且reduce后的第一个基即是L的最短向量（见下图性质）。另外格很“垂直”的话，就可以用Babai的算法解CVP问题（略）。

总结来说，只要构造出$L$和$vL = w$并且符合$||B|| ≤ \sigma(L)$的关系的话就可以解出$v$和$w$，然后利用$v$和$w$中的元素解决其他的问题。在用格攻击密码算法时基本都是这个套路，（所以略了）

个人感觉用连分数（Wiener’s）的做法和格（Lattices）的做法应该是等价的，以下给个不太严谨的证明：

能用连分数解的都可以用格解·

Theorem1： 如果给定$a、b、c、d$，有：

$$|\frac{a}{b}-\frac{c}{d}| \le \frac{1}{2d^2}$$

的话，则可以用“上述格的方法”解出$c$和$d$。

proof： 上面说的那个式子只是Legendre’s theorem换了一种表述；首先给定一个大小关系：

$$d = \Theta(2^\alpha) \\ b = \Theta(2^\beta)$$

为了拆开绝对值先考虑$a/b \ge c/d$的情况，拆绝对值后左右同乘$bd$得：

$$ad-bc \le \frac{b}{2d}$$

为了方便计算，引入一个$s$，即：

$$s = ad-bc = O(2^{\beta-\alpha-1})$$

于是就可以构造格的表达式：

$$(d, c) \begin{bmatrix} 1 & a \\ 0 & -b \\ \end{bmatrix} = (d, s)$$

记上面式子为$vM=w$，算一下可知$w \approx (2^\alpha, 2^{\beta-\alpha-1})$，为了“配平”$w$，需要做个分类讨论：

• 如果$\beta-1 \le 2\alpha$，即$s \le d$：这时需要给$M$和$w$乘上一个对角阵：

  $$D = \begin{bmatrix} 1 & 0 \\ 0 & 2^{2\alpha-\beta+1} \\ \end{bmatrix}$$

  然后就可以计算出：

  $$\sigma(MD) \approx 2^{\frac{\beta}{2}+\frac{2\alpha-\beta+1}{2}} = 2^{\alpha+\frac{1}{2}} \\ \|wD\| \approx 2^\alpha \\ \|wD\| \le \sigma(MD)$$

• 如果$2\alpha < \beta-1$，即$d<s$：算出的对角阵为：

  $$D = \begin{bmatrix} 2^{\beta-2\alpha-1} & 0 \\ 0 & 1 \\ \end{bmatrix}$$

  然后就是：

  $$\sigma(MD) \approx 2^{\frac{\beta}{2}+\frac{\beta-2\alpha-1}{2}} = 2^{\beta-\alpha-\frac{1}{2}} \\ \|wD\| \approx 2^{\beta-\alpha-1} \\ \|wD\| \le \sigma(MD)$$

即大概率可以解出$w=(d, s)$，然后$v=wM^{-1}$解出$v=(d, c)$；

$a/b < c/d$的情况其实是相似的，只是构造出来的格的表达式为：

$$(d, c) \begin{bmatrix} 1 & a \\ 0 & -b \\ \end{bmatrix} = (d, -s)$$

能用某种格构造解的都可以用连分数解·

Theorem2： 假设现在可以构造$vM=w$：

$$(d, c) \begin{bmatrix} 2^\gamma & a \\ 0 & -b \\ \end{bmatrix} = (2^\gamma d, ad-bc)$$

使得$w$为$M$中的最短向量，且$ad-bc=\Theta(2^{\gamma+1} d)$，则会有：

$$|\frac{a}{b}-\frac{c}{d}| \le \frac{1}{2d^2}$$

proof： 首先给定几个关系：

$$d = \Theta(2^\alpha) \\ b = \Theta(2^\beta) \\ ad-bc = \Theta(2^{\alpha+\gamma+1})$$

最后一个即构造$2^{\gamma+1} = \Theta(\frac{ad-bc}{d})$， （为了避免讨论$d$和$ad-bc$的大小问题，可以认为$\gamma$可以是负的，但好像这样也要做一些讨论，逃） ；可以计算出：

$$\sigma(M) \approx 2^{\frac{\beta+\gamma}{2}} \\ \|w\| \approx 2^{\alpha+\gamma+1}$$

根据Hermite’s Theorem [IMC Theorem 7.25]，有（大概-）：

$$\|w\| \le \sigma(M)$$

即：

$$\alpha+\gamma+1 \le \frac{\beta+\gamma}{2} \\ 2\alpha+\gamma+2 \le \beta \\ \alpha+(\alpha+\gamma+1) \le \beta-1$$

这个是指数上的关系，可以推出：

$$d(ad-bc) \le b/2 \\ ad-bc \le \frac{b}{2d}$$

左右同除$bd$再加个绝对值：

$$|\frac{a}{b}-\frac{c}{d}| \le \frac{1}{2d^2}$$

Wiener’s attack revisited·

有了连分数和格的等价后，就可以用格来“复现”一下Wiener攻击了，然后也可以推出一些有趣的结论；

首先根据RSA的性质，会有：

$$\phi(N) = (p-1)(q-1) = N-s \\ s = p+q-1 = \Theta(N^{1/2})$$

最后的$s=\Theta(N^{1/2})$是保证RSA安全所必须的，即$p$和$q$的规模要是一样的，不然$N$就有被分解的风险；然后攻击的主要目标是公私钥对：

$$ed \equiv 1 \pmod {\phi(N)} \\$$

把上面的代进来：

$$ed \equiv 1 \pmod {(N-s)} \\ ed + k(N-s) = 1 \\ ed + kN = ks+1$$

然后就可以构造格了：

$$(k, d) \begin{bmatrix} N^{1/2} & N \\ 0 & e \\ \end{bmatrix} = (kN^{1/2}, ks+1)$$

这里选择$(k, d)$而不是$(d, k)$是为了后面“配平”方便（事实上已经配完了-）；记上面式子$vM=w$，记大小关系：

$$e = \Theta(N^\alpha) \\ d = \Theta(N^\beta) \\ k = \Theta(N^{\alpha+\beta-1}) \\ s = \Theta(N^{1/2})$$

即可计算出：

$$\sigma(M) \approx N^{\frac{\alpha}{2}+\frac{1}{4}} \\ \|w\| \approx N^{(\alpha+\beta-\frac{1}{2})}$$

需要$\|w\| \le \sigma(M)$的话即：

$$\alpha+\beta-\frac{1}{2} \le \frac{\alpha}{2}+\frac{1}{4}$$

化简：

$$\alpha+2\beta \le 3/2$$

即其实实际会被攻击的界是：

$$ed^2 \le N^{\frac{3}{2}}$$

如果有$e=\Theta(N)$的话，才会有现在大多数人认为的$d \le N^{1/4}$；以下给个Demo code，可以拿去玩一下：

# sage
bound = 2/5
bits = 64
while True:  # gen ed = phi+1
  p = random_prime(2^bits)
  q = random_prime(2^bits)
  n = p*q
  phi = (p-1)*(q-1)

  for f in factor(phi+1)[::-1]:
    if f[0] < n^(1/2):
      if f[0] >= n^bound:
        d = f[0]
        break
  else:
    continue
  e = (d*(phi+1))//d^2
  break

print('p = %s' % p)
print('q = %s' % q)
print('n = %s' % n)
print('e = %s' % e)
print('d = %s' % d)

assert d >= n**(bound)     # of course n**(2/5) > n**(1/4)
assert e*d**2 <= n**(3/2)  # the bound with e

N = 10000
fra = (e/n).n(N).exact_rational().continued_fraction()
for i in range(len(fra)):
    k = fra.numerator(i)
    d2 = fra.denominator(i)
    
    if d2 == d:
      print(d2, d2==d)

PS：以上代码生成的是$de=\phi(n)+1$，当$ed$接近的时候$ed^2$才会变小，但$d$不会小于$N^{1/2}$

n-RSA ?·

（咕）

总结·

一个方程里如果知道所有的“大数”（包括未知的“大数”可以消去的情况），可以用Wiener’s（Legendre’s theorem）或格（Lattices）的方法解出未知的“小数”。这里的具体大小关系可能需要计算一下，一般会是 小数≤O((最大数)^{1/小未知数的数量}) （当然，只是一般，-

我个人比较偏向用格的方法（很明显上面写的几乎都是用格的-），感觉格的话会更通用（特别高维的情况），但也不排除自己对Legendre’s theorem那堆东西不是很熟了（逃

另外，遇到不等式的关系时可以多考虑Wiener’s的方法；遇到等式时可以考虑Lattices的方法。

再另外，用两种方法都会有一些 “玄学” 问题，首先是上面说过的求出来的两个数可能会和原来有一定的倍数关系；如果用格的话还需要考虑某些格的特殊性，即即使有$\|w\| \le \sigma(M)$也可能会在那个“Ball”里有很多的短向量，即$w$有可能只是个短向量而不是最短向量。

引用·

[IMC] Hoffstein J, Pipher J, Silverman J H, et al. An introduction to mathematical cryptography[M]. New York: Springer, 2008. [Wiener90] M. J. Wiener, Cryptanalysis of short RSA secret exponents", IEEE Transactions on Information Theory, vol. IT(36), pp. 553-558, 1990. [Bon99] Boneh D. Twenty years of attacks on the RSA cryptosystem[J]. Notices of the AMS, 1999, 46(2): 203-213. [OP12] Ojha N, Padhye S. Weak Keys in RSA over The Work of Blomer & May[J]. Int. J. Netw. Secur., 2012, 14(2): 80-85. [HS99] Howgrave-Graham N, Seifert J P. Extending Wiener’s attack in the presence of many decrypting exponents[C]//International Exhibition and Congress on Network Security. Springer, Berlin, Heidelberg, 1999: 153-166. [GGM16] Galbraith S D, Gebregiyorgis S W, Murphy S. Algorithms for the approximate common divisor problem[J]. LMS Journal of Computation and Mathematics, 2016, 19(A): 58-72.

[May03] May A. New RSA vulnerabilities using lattice reduction methods[D]. University of Paderborn, 2003.

[BD00] Boneh D, Durfee G. Cryptanalysis of RSA with private key d less than N/sup 0.292[J]. IEEE transactions on Information Theory, 2000, 46(4): 1339-1349.

[Gm1y] 密码学硬核笔记——扩展维纳攻击

[silent] 基于格的通用私钥攻击（RSA用了同一个d）