2022春秋杯的notKnapsack,然后由一个非预期解引出的背包问题另类解法,和Cado数域筛解DLP.
notKnapsack·
题目:task.py ( https://paste.ubuntu.com/p/ZxPHWxcSsm/ )
输出:output.txt
题目给了286组Modular Subset Product Problem(MSPP),每组有286个r k i r_{ki} r ki x i x_i x i
s k ≡ ∏ i = 1 286 x i r k i ( m o d q ) s_k \equiv \prod_{i=1}^{286} x_i r_{ki} \pmod q
s k ≡ i = 1 ∏ 286 x i r ki ( mod q )
其中q = 2 ∗ 331 ∗ p + 1 q = 2*331*p + 1 q = 2 ∗ 331 ∗ p + 1 p p p q q q r k i r_{ki} r ki s k s_k s k x i x_i x i
先说(我认为的)正解。首先如果可以解DLP的话,Subset Product Problem是可以转化为Subset Sum Problem(即背包问题Knapsack Problem)的,即设一个生成元g g g α k i \alpha_{ki} α ki g α k i ≡ r k i ( m o d q ) g^{\alpha_{ki}} \equiv r_{ki} \pmod q g α ki ≡ r ki ( mod q ) g β k ≡ s k ( m o d q ) g^{\beta_k} \equiv s_k \pmod q g β k ≡ s k ( mod q )
g β k ≡ g ∑ i = 1 286 x i α k i ( m o d φ ( q ) ) ( m o d q ) g^{\beta_k} \equiv g^{\sum_{i=1}^{286} x_i \alpha_{ki} \pmod {\varphi(q)}} \pmod q
g β k ≡ g ∑ i = 1 286 x i α ki ( mod φ ( q )) ( mod q )
其中的β k ≡ ∑ i = 1 286 x i α k i ( m o d φ ( q ) ) \beta_k \equiv \sum_{i=1}^{286} x_i \alpha_{ki} \pmod {\varphi(q)} β k ≡ ∑ i = 1 286 x i α ki ( mod φ ( q )) discrete_log开多线程也要好几个小时,前提还要电脑足够好),二是286维的Knapsack Problem并不好解。
所以得换个思路,观察一下会发现MSPP的组数和r k i r_{ki} r ki β k ≡ ∑ i = 1 286 x i α k i ( m o d φ ( q ) ) \beta_k \equiv \sum_{i=1}^{286} x_i \alpha_{ki} \pmod {\varphi(q)} β k ≡ ∑ i = 1 286 x i α ki ( mod φ ( q ))
[ α 1 , 1 α 1 , 2 ⋯ α 1 , 286 α 2 , 1 α 2 , 2 ⋯ α 2 , 286 ⋮ ⋮ ⋱ ⋮ α 286 , 1 α 286 , 2 ⋯ α 286 , 286 ] ( x 1 x 2 ⋮ x 286 ) = ( β 1 β 2 ⋮ β 286 ) ( m o d φ ( q ) ) \begin{bmatrix}
\alpha_{1,1} & \alpha_{1,2} & \cdots & \alpha_{1,286} \\
\alpha_{2,1} & \alpha_{2,2} & \cdots & \alpha_{2,286} \\
\vdots & \vdots & \ddots & \vdots \\
\alpha_{286,1} & \alpha_{286,2} & \cdots & \alpha_{286,286}
\end{bmatrix}
\begin{pmatrix}
x_1 \\ x_2 \\ \vdots \\ x_{286}
\end{pmatrix} =
\begin{pmatrix}
\beta_1 \\ \beta_2 \\ \vdots \\ \beta_{286}
\end{pmatrix}
\pmod {\varphi(q)}
⎣ ⎡ α 1 , 1 α 2 , 1 ⋮ α 286 , 1 α 1 , 2 α 2 , 2 ⋮ α 286 , 2 ⋯ ⋯ ⋱ ⋯ α 1 , 286 α 2 , 286 ⋮ α 286 , 286 ⎦ ⎤ ⎝ ⎛ x 1 x 2 ⋮ x 286 ⎠ ⎞ = ⎝ ⎛ β 1 β 2 ⋮ β 286 ⎠ ⎞ ( mod φ ( q ))
左边矩阵是个方阵,即线性方程可解。但是DLP难解的问题依然还在,这时可以借助一下Pohlig Hellman(一个解DLP的算法)的分治思路,即我其实不需要解出α k i \alpha_{ki} α ki φ ( q ) \varphi(q) φ ( q ) φ ( q ) \varphi(q) φ ( q ) φ ( q ) = 2 ∗ 331 ∗ p \varphi(q) = 2*331*p φ ( q ) = 2 ∗ 331 ∗ p 2 2 2 331 331 331
为了方便我取2 2 2 q 2 = φ ( q ) 2 q_2 = \frac{\varphi(q)}{2} q 2 = 2 φ ( q ) g g g g q 2 ≢ 1 ( m o d q ) g^{q_2} \not\equiv 1 \pmod q g q 2 ≡ 1 ( mod q ) ( g q 2 ) 2 ≡ 1 ( m o d q ) (g^{q_2})^2 \equiv 1 \pmod q ( g q 2 ) 2 ≡ 1 ( mod q )
{ ( g q 2 ) γ ≡ 1 ( m o d q ) , if γ is even ( g q 2 ) γ ≢ 1 ( m o d q ) , if γ is odd \begin{cases}
(g^{q_2})^\gamma \equiv 1 \pmod q, & \text{if $\gamma$ is even} \\
(g^{q_2})^\gamma \not\equiv 1 \pmod q, & \text{if $\gamma$ is odd}
\end{cases}
{ ( g q 2 ) γ ≡ 1 ( mod q ) , ( g q 2 ) γ ≡ 1 ( mod q ) , if γ is even if γ is odd
于是算一下所有的r k i q 2 ( m o d q ) r_{ki}^{q_2} \pmod q r ki q 2 ( mod q ) α k i \alpha_{ki} α ki β k \beta_k β k
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 q = 210767327475911131359308665806489575328083 with open ('./output.txt' , 'r' ) as f: data = f.read() data = eval (data) q2 = (q-1 ) // 2 g2 = pow (2 , q2, q) A = zero_matrix(GF(2 ), len (data)) s = vector(GF(2 ), [0 for _ in range (len (data))]) for i in range (len (data)): for j in range (len (data[i][0 ])): r2 = pow (data[i][0 ][j], q2, q) if r2 == 1 : A[i, j] = 0 elif r2 == g2: A[i, j] = 1 else : print ('???' ) exit(-1 ) s2 = pow (data[i][1 ], q2, q) if s2 == 1 : s[i] = 0 elif s2 == g2: s[i] = 1 else : print ('????' ) x = A.solve_right(s) print (x)import libnumm = int ('' .join([str (xi) for xi in x]), 2 ) flag = libnum.n2s(int (m)) flag = 'flag{%s}' % flag.decode() print (flag)
Cado-nfs与DLP·
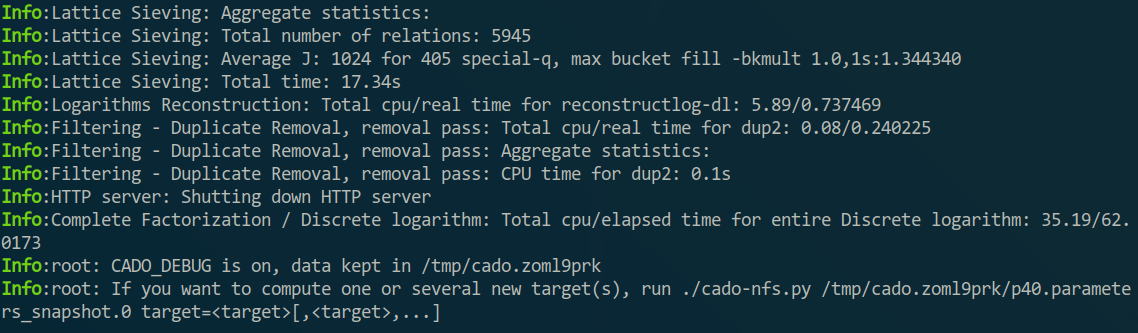
Cado-nfs 是一个基于数域筛法(Number Field Sieve ,NFS)的整数分解工具,但是可以用来解较小数的DLP,而且速度意外的快(拿我的渣机作例子,解上面说的一组MSPP的287个DLP需要大概半小时),Cado解DLP的用法在这里 有介绍。代码可以在官方的GitLab下载,下载完make一下就好了(文档有说,略)。
拿这一题作例子,即q = 210767327475911131359308665806489575328083 q=210767327475911131359308665806489575328083 q = 210767327475911131359308665806489575328083 q − 1 = 2 ∗ 331 ∗ 318379648755152766403789525387446488411 q-1=2*331*318379648755152766403789525387446488411 q − 1 = 2 ∗ 331 ∗ 318379648755152766403789525387446488411
1 ./cado-nfs.py -dlp -ell=318379648755152766403789525387446488411 210767327475911131359308665806489575328083
-dlp就是用Cado解DLP而不是分解的意思,-ell后面接q − 1 q-1 q − 1 q − 1 q-1 q − 1 q q q
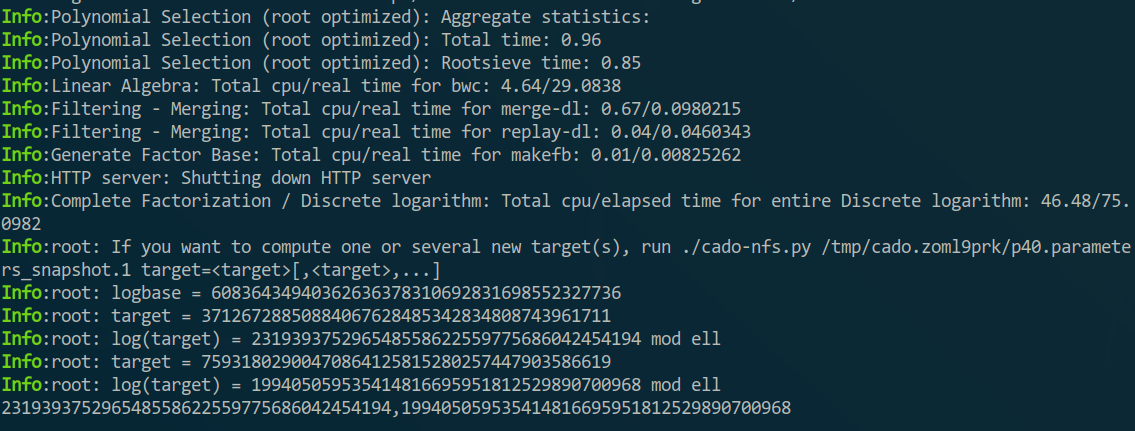
接下来如果我想解37126728850884067628485342834808743961711 37126728850884067628485342834808743961711 37126728850884067628485342834808743961711 75931802900470864125815280257447903586619 75931802900470864125815280257447903586619 75931802900470864125815280257447903586619 r 11 r_{11} r 11 r 12 r_{12} r 12
1 ./cado-nfs.py /tmp/cado.zoml9prk/p40.parameters_snapshot.0 target=37126728850884067628485342834808743961711,75931802900470864125815280257447903586619
很好理解,就是target后面接要解的值,多个值用逗号隔开。这里要提一下的是,Cado似乎是不能指定基底(生成元g g g
运行完后会给出结果和使用的基底logbase = 60836434940362636378310692831698552327736。(PS:解这两个用了14秒)
上面说的是在命令行运行的,但是如果用Cado来解notKnapsack的话,一大堆target在命令行跑不太实际,然后Cado好像没给API调用?所以粗略写了个脚本(懒得逆了,逃):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 import osCADO_PATH = 'path/to/cado-nfs/' CADO_CMD = './cado-nfs.py --screenlog=INFO /tmp/cado.xxxxxxxx/p40.parameters_snapshot.0 target=%s' with open ('output.txt' , 'r' ) as f: data = f.read() data = eval (data) os.chdir(CADO_PATH) for i in range (len (data))[0 :N]: print ('Doing - %d' % i) target = '' for ri in data[i][0 ]: target += str (ri) + ',' s = data[i][1 ] target += str (s) cmd = CADO_CMD % target print (cmd) os.system(cmd)
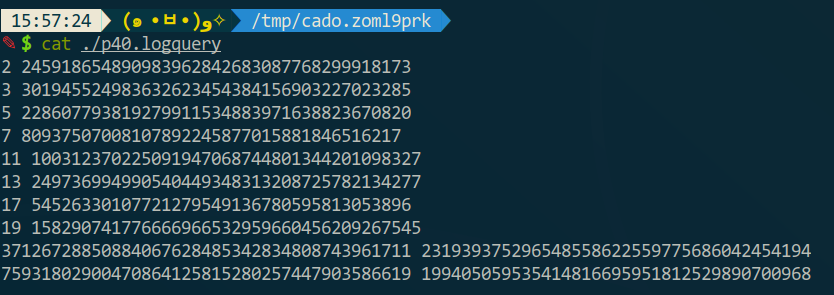
Cado跑的每一条结果都会以下面格式储存在/tmp/cado.xxxxxxxx/pxx.logquery中(就是刚才说的中间文件的文件夹),所以可以选择运行完后直接读logquery获取结果。
1 2 3 4 5 6 7 8 with open ('/tmp/cado.xxxxxxxx/pxx.logquery' , 'r' ) as f: query = f.read().split('\n' )[:-1 ] query = [[int (qi) for qi in q.split(' ' )] for q in query] logs = {} for q in query: logs[q[0 ]] = q[1 ]
(关于NFS的理论先留个坑,有空补,逃)
关于Knapsack·
在很久以前 我有提到过带模的背包问题的解法,当时说的是推出有∥ w D ∥ ≤ σ ( M D ) \|wD\| ≤ \sigma(MD) ∥ w D ∥ ≤ σ ( M D )
这其中有两个原因,一个是LLL算法其实并不能解SVP问题,它解的是apprSVP,即设格的最短向量长度是λ 1 \lambda_1 λ 1 b 1 b_1 b 1 ∥ b 1 ∥ ≤ ( δ − 1 4 ) 2 / ( n − 1 ) ⋅ λ 1 \|b_1\| \le (\delta-\frac{1}{4})^{2/(n-1)} · \lambda_1 ∥ b 1 ∥ ≤ ( δ − 4 1 ) 2/ ( n − 1 ) ⋅ λ 1 δ \delta δ n n n b 1 b_1 b 1 ( δ − 1 4 ) 2 / ( n − 1 ) (\delta-\frac{1}{4})^{2/(n-1)} ( δ − 4 1 ) 2/ ( n − 1 ) n n n b 1 b_1 b 1 BKZ然后设置一个较大的block_size缓解,但是block_size越大运行时间越长(原文是“running time increases double exponentially with block_size”,可参考这里 );而且我调Sage的BKZ维度过大的话会what(): infinite loop in babai- -
第二个原因是,当维度增大时,解背包问题用到的格的λ 2 − G a p \lambda_2\rm{-Gap} λ 2 − Gap λ 1 \lambda_1 λ 1 λ 2 \lambda_2 λ 2 λ i \lambda_i λ i ( δ − 1 4 ) 2 / ( n − 1 ) ⋅ λ 1 (\delta-\frac{1}{4})^{2/(n-1)} · \lambda_1 ( δ − 4 1 ) 2/ ( n − 1 ) ⋅ λ 1 λ 2 − G a p \lambda_2\rm{-Gap} λ 2 − Gap
但是,这样子摁构造一个新的格是挺难的,所以接下来我会引入一个新的假设,即假设我知道同一个明文对应多组不同公钥的背包加密的结果,观察会发现notKnapsack的β k ≡ ∑ i = 1 n x i α k i ( m o d φ ( q ) ) \beta_k \equiv \sum_{i=1}^{n} x_i \alpha_{ki} \pmod {\varphi(q)} β k ≡ ∑ i = 1 n x i α ki ( mod φ ( q ))
假设我用Cado解了n r n_r n r β k = ∑ i = 1 n x i α k i − t k φ ( q ) \beta_k = \sum_{i=1}^{n} x_i \alpha_{ki} - t_k\varphi(q) β k = ∑ i = 1 n x i α ki − t k φ ( q ) k = 1 , 2 , . . . , n r k=1, 2, ..., n_r k = 1 , 2 , ... , n r β k \beta_k β k α k i \alpha_{ki} α ki φ ( q ) \varphi(q) φ ( q ) L ( B ) L(B) L ( B )
B = [ 2 α 1 , 1 α 2 , 1 ⋯ α n r , 1 2 α 1 , 2 α 2 , 2 ⋯ α n r , 2 ⋱ ⋮ ⋮ ⋱ ⋮ 2 α 1 , n α 2 , n ⋯ α n r , n φ ( q ) φ ( q ) ⋱ φ ( q ) 1 1 ⋯ 1 β 1 β 2 ⋯ β n r − 1 ] ( n + n r + 1 ) ∗ ( n + n r + 1 ) \begin{align}
B =
\begin{bmatrix}
2 & & & & \alpha_{1, 1} & \alpha_{2, 1} & \cdots & \alpha_{n_r, 1} & \\
& 2 & & & \alpha_{1, 2} & \alpha_{2, 2} & \cdots & \alpha_{n_r, 2} & \\
& & \ddots & & \vdots & \vdots & \ddots & \vdots \\
& & & 2 & \alpha_{1, n} & \alpha_{2, n} & \cdots & \alpha_{n_r, n} & \\
& & & & \varphi(q) & & & & \\
& & & & & \varphi(q) & & & \\
& & & & & & \ddots & & \\
& & & & & & & \varphi(q) & \\
1 & 1 & \cdots & 1 & \beta_1 & \beta_2 & \cdots & \beta_{n_r} & -1
\end{bmatrix}_{(n+n_r+1)*(n+n_r+1)} \\
\end{align}
B = ⎣ ⎡ 2 1 2 1 ⋱ ⋯ 2 1 α 1 , 1 α 1 , 2 ⋮ α 1 , n φ ( q ) β 1 α 2 , 1 α 2 , 2 ⋮ α 2 , n φ ( q ) β 2 ⋯ ⋯ ⋱ ⋯ ⋱ ⋯ α n r , 1 α n r , 2 ⋮ α n r , n φ ( q ) β n r − 1 ⎦ ⎤ ( n + n r + 1 ) ∗ ( n + n r + 1 )
使得
v B = ( x 1 , x 2 , . . . , x n , t 1 , t 2 , . . . , t n r , − 1 ) ⋅ B = ( 2 x 1 − 1 , 2 x 2 − 1 , . . . , 2 x n − 1 , 0 , 0 , . . . , 0 , 1 ) = w vB = (x_1, x_2, ..., x_n, t_1, t_2, ..., t_{n_r}, -1)·B \\
= (2x_1-1, 2x_2-1, ..., 2x_n-1, 0, 0, ..., 0, 1) = w
v B = ( x 1 , x 2 , ... , x n , t 1 , t 2 , ... , t n r , − 1 ) ⋅ B = ( 2 x 1 − 1 , 2 x 2 − 1 , ... , 2 x n − 1 , 0 , 0 , ... , 0 , 1 ) = w
首先∥ w ∥ = n + 1 \|w\|=\sqrt{n+1} ∥ w ∥ = n + 1 ∥ w ∥ ≤ σ ( L ( B ) ) \|w\| ≤ \sigma(L(B)) ∥ w ∥ ≤ σ ( L ( B )) n = 32 n=32 n = 32 n n n
n r n_r n r λ 1 \lambda_1 λ 1 λ 2 \lambda_2 λ 2
1
5.74456265
50.0499750
2
5.74456265
675.983728
3
5.74456265
9461.71512
4
5.74456265
99343.2373
5
5.74456265
871867.823
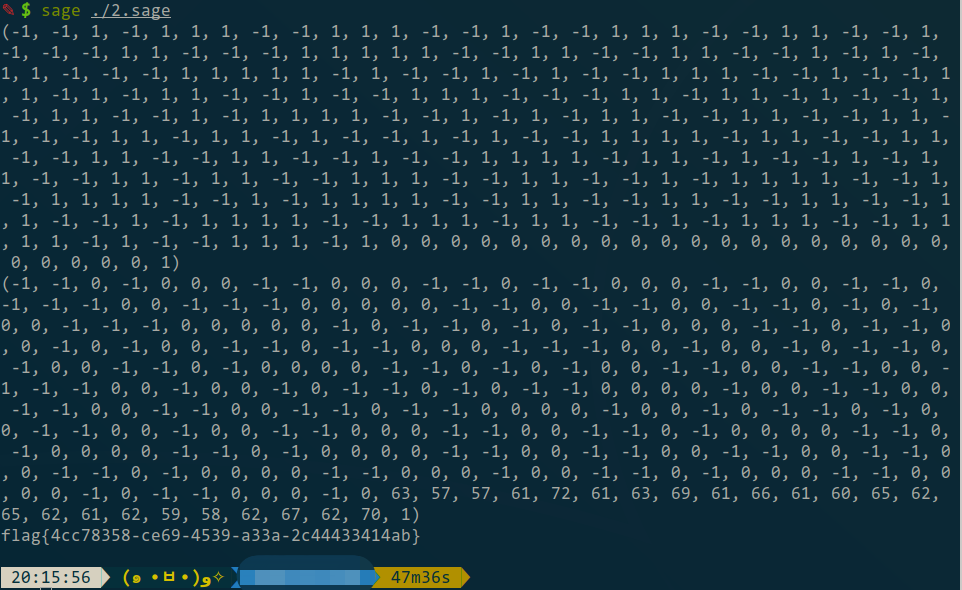
明显n r n_r n r λ 2 − G a p \lambda_2\rm{-Gap} λ 2 − Gap n r = 24 n_r=24 n r = 24
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 q = 210767327475911131359308665806489575328083 phiq = 318379648755152766403789525387446488411 with open ('/tmp/cado.xul9ujy8/p40.logquery' , 'r' ) as f: query = f.read().split('\n' )[:-1 ] query = [[int (qi) for qi in q.split(' ' )] for q in query] logs = {} for q in query: logs[q[0 ]] = q[1 ] with open ('./../../output.txt' , 'r' ) as f: data = f.read() data = eval (data) rs = [] ss = [] for i in range (1 , 25 ): tmp = [] for r in data[i][0 ]: tmp.append(logs[r]) rs.append(tmp) ss.append(logs[data[i][1 ]]) C = 131 kk = 2 n = len (data[0 ][0 ]) nr = len (rs) Mt = zero_matrix(n + nr + 1 ) for i in range (n): Mt[i, i] = kk Mt[-1 , i] = kk // 2 for i in range (nr): Mt[i+n, i+n] = phiq for j in range (n): Mt[j, i+n] = rs[i][j] Mt[-1 , i+n] = ss[i] Mt[-1 , -1 ] = kk // 2 for i in range (nr): for j in range (len (Mt[0 ])): Mt[j, i+n] *= C L = Mt.LLL() print (L[0 ])xs = Mt.solve_left(L[0 ]) print (xs)import libnumx = [abs (x) for x in xs[:n]] m = int ('' .join([str (xi) for xi in x]), 2 ) flag = libnum.n2s(int (m)) flag = 'flag{%s}' % flag.decode() print (flag)