很少见的置换群的题目，这次是个开平方，本来以为只有两个解，然后开出了2^20+个解。。。

前置知识·

置换群·

首先什么是置换（Permutation）应该好懂，比如我对(1,2,3)(1, 2, 3)这三个元素做置换

1
2
3
import itertools  
print(list(itertools.permutations([1, 2, 3])))      
# [(1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1)]

就会有以上六种情况（其实就是排列组合中的排列，Permutation又可译作排列）

假设这三个集合组成的元素是X={1,2,3}X = \{1, 2, 3\}，我们会称XX排列出来的以上六种情况组成一个对称群SXS_X（Symmetric Group），然后SXS_X的（其中一个）子群就被称作置换群（Permutation Group）

如果XX是像上面那样从11开始，递增到nn的集合X={1,2,⋯ ,n}X = \{1, 2, \cdots, n\}，则通常会把SXS_X简写成SnS_n，又称做nn阶对称群（虽然这个“阶”有点怪怪的，英文中说的是“We call this group the symmetric group on n letters.”）

置换群中的一个元素是一个置换，比如

σ=(123231)\sigma = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix}

表示一个置换，表示把11换做22，把22换作33，把33换做11，或者写作

σ(1)=2σ(2)=3σ(3)=1\sigma(1) = 2 \\ \sigma(2) = 3 \\ \sigma(3) = 1

群操作·

再来看群操作，置换群中的群操作是置换的复合，通常用符号∘\circ表示

(σ∘τ)(x)=σ(τ(x))(\sigma \circ \tau)(x) = \sigma(\tau(x))

以上表示的意思是先做τ\tau置换，再做σ\sigma置换，通常为了方便也会省略∘\circ直接写成στ\sigma\tau

群元也可以自己和自己复合，比如σσ\sigma \sigma就是σ\sigma置换做两遍，也会写作σ2\sigma^2

在SageMath代码中就是直接用*表示群操作，用^表示自己复合多少次了，如

1
2
3
4
5
6
G = Permutations(3)
g = G.random_element()	# [3, 1, 2]
h = G.random_element()	# [3, 2, 1]
print(g * h)	# [1, 3, 2]
print(g^2)	# [2, 3, 1]
print(g^3)	# [1, 2, 3]

以上G就是S3S_3的置换群，g和h是随机选的群中的两个元素，其中[3, 1, 2]表示的是(123312)\begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix}，只是为了方便把第一排省略了

在这个例子中可以看到g的阶是33，因为[1, 2, 3]即是单位元，顺带提一句，置换群的群阶是其对称群的阶的一个因子，而SnS_n的阶是n!n!

回圈表述·

最后来说说群元的另一种表述方法，上面把11~nn所有置换情况列出来的表述方法叫列表法，通常只是为了看起来直观，而在代数中更常用的是使用回圈（Cycles）表示一个置换

假设在一个置换σ\sigma中存在以下情况：

σ(a0)=a1σ(a1)=a2⋮σ(ak−1)=a0\sigma(a_0) = a_1 \\ \sigma(a_1) = a_2 \\ \vdots \\ \sigma(a_{k-1}) = a_0

那么在σ\sigma中就存在一个长度为kk的回圈，这个圈写作(a0,a1,⋯ ,ak−1)(a_0, a_1, \cdots, a_{k-1})（PS：所以圆括号是表示回圈，不能乱用）

PS：有的文章也会从下标为11的a1a_1开始，不过我习惯00开始，而且一会也更好说明

举个复杂点的栗子，比如

σ=(12345672413657)\sigma = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ 2 & 4 & 1 & 3 & 6 & 5 & 7 \end{pmatrix}

那么在σ\sigma中就存在三个回圈：(1,2,4,3)(1,2,4,3)、(5,6)(5,6)和(7)(7)，不熟悉的建议在纸上画一下，看看是不是会连成一个闭合的圈，比较特殊的是单个元素也认为可以自己成一个圈

所以σ\sigma也可以用回圈的方法表述为：σ=(1,2,4,3)(5,6)(7)\sigma = (1, 2, 4, 3)(5, 6)(7)，通常长度为11的回圈可以省略不写，所以可以简写为σ=(1,2,4,3)(5,6)\sigma = (1, 2, 4, 3)(5, 6)

在SageMath中如果使用PermutationGroupElement定义一个置换群元的话，打印出来会是回圈的表述，而不是Permutations的列表表述，如

1
2
3
PermutationGroupElement([2, 4, 1, 3, 6, 5, 7])		# (1,2,4,3)(5,6)
PermutationGroupElement('(1, 2, 4, 3)(5, 6)(7)')	# (1,2,4,3)(5,6)
PermutationGroupElement('(1, 2, 4, 3)(5, 6)')		# (1,2,4,3)(5,6)

置换群开方·

所谓开方，即知道一个置换群元和自己的复合σ2\sigma^2，求这个群元σ\sigma

网上翻一下可以在StackExchange上翻到这个帖子，里面有说如何找一个平方根，但并没有把情况说全，可以参考着推一下

平方操作·

首先看一下“平方”操作会发生什么，如前文所说的，平方其实就是自己跟自己复合，也就σ2(x)=σ(σ(x))\sigma^2(x) = \sigma(\sigma(x))，即对于每个数xx，做了两次σ\sigma的置换

举个栗子

σ=(12345672413675)=(1,2,4,3)(5,6,7)\sigma = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ 2 & 4 & 1 & 3 & 6 & 7 & 5 \end{pmatrix} = (1,2,4,3)(5,6,7)

简单算个平方

x1234567()σ(x)2413675(1,2,4,3)(5,6,7)σ2(x)4321756(1,4)(2,3)(5,7,6)\begin{array}{c|ccccccc|c} x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & () \\ \sigma(x) & 2 & 4 & 1 & 3 & 6 & 7 & 5 & (1,2,4,3)(5,6,7) \\ \sigma^2(x) & 4 & 3 & 2 & 1 & 7 & 5 & 6 & (1,4)(2,3)(5,7,6) \end{array}

拿x=1x=1做栗子，本来σ\sigma中是1→21 \to 2、2→42 \to 4，现在σ2\sigma^2是连着做两次σ\sigma，即1→2→41 \to 2 \to 4，省略中间过程的22，即1→41 \to 4，其他情况类似，可以看上表的最后一行

接下来看回圈的表述，σ\sigma做两次置换其实等同于σ\sigma中的每个回圈都分别做两次置换， 因为这些回圈只是把σ\sigma拆分成几个部分，即令σ=σ0σ1⋯σs−1\sigma = \sigma_0\sigma_1\cdots\sigma_{s-1}，则σ2=σ02σ12⋯σs−12\sigma^2 = \sigma_0^2\sigma_1^2\cdots\sigma_{s-1}^2

所以只用分析在平方过程中的回圈会发生什么就好了，如上面所说，回圈的平方也就是在这个回圈中转两下，或者说做两个置换，即令σi=(a0,a1,⋯ ,ak−1)\sigma_i = (a_0, a_1, \cdots, a_{k-1})，则

σi2(a0)=a2σi2(a1)=a3⋮σi2(aj)=aj+2(modk)\sigma_i^2(a_0) = a_2 \\ \sigma_i^2(a_1) = a_3 \\ \vdots \\ \sigma_i^2(a_j) = a_{j + 2 \pmod k}

到这里根据长度kk的奇偶性会出现两种情况：

  • 如果kk是偶数，由于GCD(2,k)=2\text{GCD}(2, k) = 2，所以σi2\sigma_i^2会被拆分为σi2=(a0,a2,⋯ ,ak−2)(a1,a3,⋯ ,ak−1)\sigma_i^2 = (a_0, a_2, \cdots, a_{k-2})(a_1, a_3, \cdots, a_{k-1})两个圈，这两个圈的长度相同且都为k2\frac{k}{2}
  • 如果kk是奇数，由于GCD(2,k)=1\text{GCD}(2, k) = 1，所以σi2\sigma_i^2还是一个长度为kk的圈，只是里面元素的顺序会改变，变为σi2=(a0,a2,⋯ ,ak−3,ak−1,a1,a3,⋯ ,ak−4,ak−2)\sigma_i^2 = (a_0, a_2, \cdots, a_{k-3}, a_{k-1}, a_1, a_3, \cdots, a_{k-4}, a_{k-2})

代进上面的栗子，(1,2,4,3)(1,2,4,3)是偶数圈，所以被拆分成(1,4)(2,3)(1,4)(2,3)两个圈，(5,6,7)(5,6,7)是奇数圈，所以没有拆分，但是顺序变成了(5,7,6)(5,7,6)

开方操作·

简单地说，开方就是上面平方操作的逆，但实际情况会复杂一点，首先不妨令τ=σ2\tau = \sigma^2

奇数圈·

先看比较简单的奇数圈，由于奇数圈在平方过程中没被拆分且长度不变，所以如果在σ2\sigma^2中发现有奇数圈τi\tau_i的话，那它就可能是σ\sigma中的某个同长度的奇数圈σj\sigma_j平方所得，即τi=σj2\tau_i = \sigma_j^2。如果还能发现，在τ\tau的所有圈中仅有这个圈的长度是∣τi∣|\tau_i|的话，那就石锤了，τi\tau_i肯定是σ\sigma中的某个同长度的奇数圈σj\sigma_j平方所得

假设真的有σj2=τi\sigma_j^2 = \tau_i，这时只需要更改一下τi\tau_i的顺序即可恢复σj\sigma_j，不妨假设这俩长度都是kk，令

τi=(r0,r1,⋯ ,rk−1)σj=(a0,a1,⋯ ,ak−1)\tau_i = (r_0, r_1, \cdots, r_{k-1}) \\ \sigma_j = (a_0, a_1, \cdots, a_{k-1})

根据τi=σj2\tau_i = \sigma_j^2和kk是奇数，由上面内容可得

τi=σj2=(a0,a2,⋯ ,ak−3,ak−1,a1,a3,⋯ ,ak−4,ak−2)=(r0,r1,⋯ ,rk−1)\begin{aligned} \tau_i &= \sigma_j^2 \\ &= (a_0, a_2, \cdots, a_{k-3}, a_{k-1}, a_1, a_3, \cdots, a_{k-4}, a_{k-2}) \\ &= (r_0, r_1, \cdots, r_{k-1}) \end{aligned}

把两个表列出来对一下

a0a2⋯ak−3ak−1a1a3⋯ak−4ak−2r0r1⋯rk−12−1rk−12rk−12+1rk−12+2⋯rk−2rk−1\begin{array}{cccccccccc} a_0 & a_2 & \cdots & a_{k-3} & a_{k-1} & a_1 & a_3 & \cdots & a_{k-4} & a_{k-2} \\ r_0 & r_1 & \cdots & r_{\frac{k-1}{2}-1} & r_{\frac{k-1}{2}} & r_{\frac{k-1}{2} + 1} & r_{\frac{k-1}{2} + 2} & \cdots & r_{k-2} & r_{k-1} \end{array}

换个好看点的表达，折叠一下：

a0a2⋯⋯ak−3ak−1r0r1⋯⋯rk−12−1rk−12a1a3⋯ak−4ak−2rk−12+1rk−12+2⋯rk−2rk−1\begin{array}{cccccc} a_0 & a_2 & \cdots & \cdots & a_{k-3} & a_{k-1} \\ r_0 & r_1 & \cdots & \cdots & r_{\frac{k-1}{2}-1} & r_{\frac{k-1}{2}} \\ \hline a_1 & a_3 & \cdots & a_{k-4} & a_{k-2} \\ r_{\frac{k-1}{2} + 1} & r_{\frac{k-1}{2} + 2} & \cdots & r_{k-2} & r_{k-1} \end{array}

把aa行的顺序排一下即得σj=(r0,rk−12+1,r1,rk−12+2,⋯ ,rk−12−1,rk−1,rk−12)\sigma_j = (r_0, r_{\frac{k-1}{2} + 1}, r_1, r_{\frac{k-1}{2} + 2}, \cdots, r_{\frac{k-1}{2} - 1}, r_{k-1}, r_{\frac{k-1}{2}})，这在数学上表达会有点麻烦，但在代码中就是上面取一个下面取一个这样就好了，比如

1
2
3
4
5
6
7
8
9
10
11
12
13
def sqrtOdd(oddCircles):
  Ptmp = ''
  for oc in oddCircles:
    k = len(oc)
    assert k % 2 == 1
    k = (k - 1) // 2
    tmp = []
    for i in range(k):
      tmp += [oc[i]]
      tmp += [oc[k+i+1]]
    tmp += [oc[k]]
    Ptmp += str(tuple(tmp))
  return Ptmp

偶数圈·

再来看偶数圈的情况，因为偶数圈平方会产生分裂，所以情况会变得非常复杂

首先如果在τ\tau的所有回圈中找到两个回圈，比如τi0\tau_{i_0}和τi1\tau_{i_1}，拥有相同的长度k2\frac{k}{2}，那么其可能由σ\sigma中的一个长度为kk的回圈σj\sigma_j平方产生，即σj2=τi0τi1\sigma_j^2 = \tau_{i_0} \tau_{i_1}

如果这个长度k2\frac{k}{2}是偶数，那么就石锤了，因为奇数圈平方只会产生奇数圈。如果k2\frac{k}{2}是奇数，那么可能会产生误会，即τi0\tau_{i_0}和τi1\tau_{i_1}其实是由σ\sigma中两个长度为k2\frac{k}{2}的奇数圈σj0\sigma_{j_0}和σj1\sigma_{j_1}平方产生

假设真的有σj2=τi0τi1\sigma_j^2 = \tau_{i_0} \tau_{i_1}，令

τi0=(r0,0,r0,1,⋯ ,r0,k2−1)τi1=(r1,0,r1,1,⋯ ,r1,k2−1)σj=(a0,a1,⋯ ,ak−1)\tau_{i_0} = (r_{0, 0}, r_{0, 1}, \cdots, r_{0, \frac{k}{2}-1}) \\ \tau_{i_1} = (r_{1, 0}, r_{1, 1}, \cdots, r_{1, \frac{k}{2}-1}) \\ \sigma_j = (a_0, a_1, \cdots, a_{k-1})

那么根据上面平方的分析就会有

τi0τi1=σj2=(a0,a2,⋯ ,ak−2)(a1,a3,⋯ ,ak−1)τi0=(a0,a2,⋯ ,ak−2)τi1=(a1,a3,⋯ ,ak−1)\begin{aligned} \tau_{i_0} \tau_{i_1} &= \sigma_j^2 = (a_0, a_2, \cdots, a_{k-2})(a_1, a_3, \cdots, a_{k-1}) \\ \tau_{i_0} &= (a_0, a_2, \cdots, a_{k-2}) \\ \tau_{i_1} &= (a_1, a_3, \cdots, a_{k-1}) \end{aligned}

然后接下来似乎是直接

τi0=(r0,0,r0,1,⋯ ,r0,k2−1)=(a0,a2,⋯ ,ak−2)τi1=(r1,0,r1,1,⋯ ,r1,k2−1)=(a1,a3,⋯ ,ak−1)\tau_{i_0} = (r_{0, 0}, r_{0, 1}, \cdots, r_{0, \frac{k}{2}-1}) = (a_0, a_2, \cdots, a_{k-2}) \\ \tau_{i_1} = (r_{1, 0}, r_{1, 1}, \cdots, r_{1, \frac{k}{2}-1}) = (a_1, a_3, \cdots, a_{k-1}) \\

就可以了，但，在回圈的表述上有一个坑，举个栗子，比如现在有一个回圈是(b0,b1,b2)(b_0, b_1, b_2)，那么其实

(b0,b1,b2)=(b1,b2,b0)=(b2,b0,b1)(b_0, b_1, b_2) = (b_1, b_2, b_0) = (b_2, b_0, b_1)

以上三个其实是同一个回圈的不同表述，可以用代码check一下，PermutationGroupElement会默认把最小的元素放在第一个位置

1
2
PermutationGroupElement('(2, 3, 1)')	# (1,2,3)
PermutationGroupElement('(3, 1, 2)')	# (1,2,3)

这在单个回圈使用的时候其实是没有问题的，但是在两个回圈组合的时候就会有问题，还是先从栗子入手，比如现在

τi0=(1,3,7,4)τi1=(2,9,8,6)\tau_{i_0} = (1,3,7,4) \\ \tau_{i_1} = (2,9,8,6)

如果直接套上面结果的话，会有

(a0,a2,a4,a6)=(1,3,7,4)(a1,a3,a5,a7)=(2,9,8,6)(a_0, a_2, a_4, a_6) = (1,3,7,4) \\ (a_1, a_3, a_5, a_7) = (2,9,8,6)

然后得出σj=(1,2,3,9,7,8,4,6)\sigma_j = (1, 2, 3, 9, 7, 8, 4, 6)

但其实还能这样

(a0,a2,a4,a6)=(1,3,7,4)(a1,a3,a5,a7)=(9,8,6,2)(a_0, a_2, a_4, a_6) = (1,3,7,4) \\ (a_1, a_3, a_5, a_7) = (9,8,6,2)

然后得出σj=(1,9,3,8,7,6,4,2)\sigma_j = (1, 9, 3, 8, 7, 6, 4, 2) ，明显这是一个不同的解

类似地还可以得出σj=(1,8,3,6,7,2,4,9)\sigma_j = (1,8,3,6,7,2,4,9)和σj=(1,6,3,2,7,9,4,8)\sigma_j = (1,6,3,2,7,9,4,8)两个不同的解

那如何解呢，还是以这个栗子，先画个图，可以把问题转化为下面的问题，现在有(1,3,7,4)(1,3,7,4)和(2,9,8,6)(2,9,8,6)两个轮盘

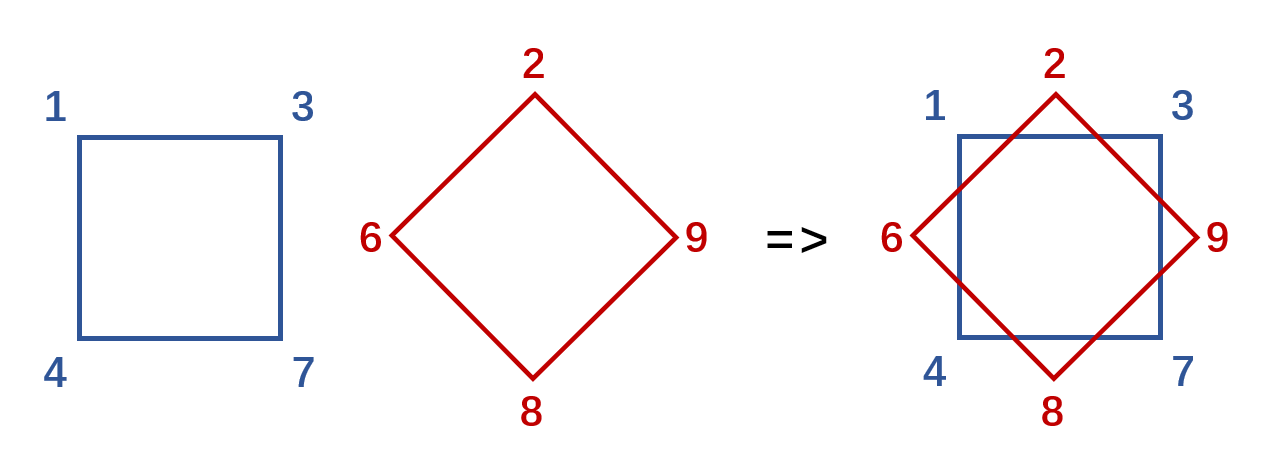
把他们重叠在一起，然后顺时针读数就可以得到(1,2,3,9,7,8,4,6)(1, 2, 3, 9, 7, 8, 4, 6)

现在两个轮盘都是可以转动的，在所有转动情况中，总共有多少种读数呢，答案是，只需要固定其中一个轮盘，然后转动另一个轮盘就好了，比如我转动红色的

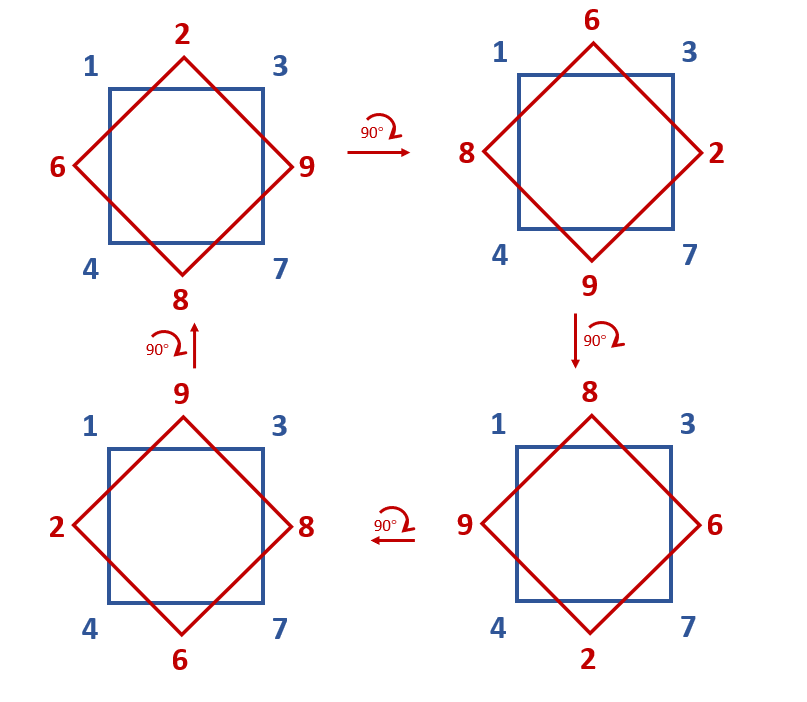
最后一共有四种情况，就是上面的四个解

再回到

τi0τi1=σj2=(r0,0,r0,1,⋯ ,r0,k2−1)(r1,0,r1,1,⋯ ,r1,k2−1)\tau_{i_0} \tau_{i_1} = \sigma_j^2 = (r_{0, 0}, r_{0, 1}, \cdots, r_{0, \frac{k}{2}-1}) (r_{1, 0}, r_{1, 1}, \cdots, r_{1, \frac{k}{2}-1})

按照上面轮盘分析，一共会有k2\frac{k}{2}个解，引入一个变量l=0,1,...,k2l = 0, 1, ..., \frac{k}{2}，假设τi0\tau_{i_0}是那个定死的轮盘，τi1\tau_{i_1}是那个转动的轮盘，即有

τi0=(r0,0,r0,1,⋯ ,r0,k2−1)=(a0,a2,⋯ ,ak−2)τi1=(r1,0,r1,1,⋯ ,r1,k2−1)=(a1+2l(modk2),a3+2l(modk2),⋯ ,ak−1+2l(modk2))\begin{aligned} \tau_{i_0} &= (r_{0, 0}, r_{0, 1}, \cdots, r_{0, \frac{k}{2}-1}) \\ &= (a_0, a_2, \cdots, a_{k-2}) \\ \tau_{i_1} &= (r_{1, 0}, r_{1, 1}, \cdots, r_{1, \frac{k}{2}-1}) \\ &= (a_{1+2l \pmod {\frac{k}{2}}}, a_{3+2l \pmod {\frac{k}{2}}}, \cdots, a_{k-1+2l \pmod {\frac{k}{2}}}) \\ \end{aligned}

然后重排aa的顺序，即可得σj\sigma_j，用上面的写法会比较难排，不妨换个思路，我不转aa而是转rr，即

(a1,a3,⋯ ,ak−1)=(r1,0+l(modk2),r1,1+l(modk2),⋯ ,r1,k2−1+l(modk2))(a_1, a_3, \cdots, a_{k-1}) = (r_{1, 0+l \pmod {\frac{k}{2}}}, r_{1, 1+l \pmod {\frac{k}{2}}}, \cdots, r_{1, \frac{k}{2}-1+l \pmod {\frac{k}{2}}})

列表

a0a2⋯ak−2r0,0r0,1⋯r0,k2−1a1a3⋯ak−1r1,0+l(modk2)r1,1+l(modk2)⋯r1,k2−1+l(modk2)\begin{array}{cccc} a_0 & a_2 & \cdots & a_{k-2} \\ r_{0, 0} & r_{0, 1} & \cdots & r_{0, \frac{k}{2}-1} \\ \hline a_1 & a_3 & \cdots & a_{k-1} \\ r_{1, 0+l \pmod {\frac{k}{2}}} & r_{1, 1+l \pmod {\frac{k}{2}}} & \cdots & r_{1, \frac{k}{2}-1+l \pmod {\frac{k}{2}}} \end{array}

即可排出σj=(r0,0,r1,0+l(modk2),r0,1,r1,1+l(modk2),⋯ ,r0,k2−1,r1,k2−1+l(modk2))\sigma_j = (r_{0, 0}, r_{1, 0+l \pmod {\frac{k}{2}}}, r_{0, 1}, r_{1, 1+l \pmod {\frac{k}{2}}}, \cdots, r_{0, \frac{k}{2}-1}, r_{1, \frac{k}{2}-1+l \pmod {\frac{k}{2}}})

同样也是代码会比数学上好搞，参考代码（变量名会有点不一样，我懒得改了-）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def sqrtEven(evenCircles):
  Ptmp = []
  if evenCircles == []:
    return []
  assert len(evenCircles) == 2
  assert len(evenCircles[0]) == len(evenCircles[1])
  k = len(evenCircles[0])
  if k % 2 == 1:
    Ptmp += [sqrtOdd([evenCircles[0]]) + sqrtOdd([evenCircles[1]])]
  for i in range(k):
    tmp = []
    for j in range(k):
      tmp += [evenCircles[0][j]]
      tmp += [evenCircles[1][(i+j)%k]]
    Ptmp += [str(tuple(tmp))]
  return Ptmp

BRICS+的sqrt·

题目：sqrt.zip

题目不长，就是给定S256S_{256}的置换群的群元P的平方，求P，根据上面分析列出所有情况遍历flag即可

首先获得P的所有回圈，使用PermutationGroupElement(P2)打印即可，但有个坑是它会省略长度为11的回圈，需要自己补回去

然后结果是：有11个长度7575的回圈、22个长度8282的回圈、33个长度33的回圈和88个长度11的回圈

  • 长度7575的明显是某个长度7575的回圈平方所得
  • 那两个长度8282的也明显是某个长度164164的回圈平方所得
  • 那33个长度为33的就有点麻烦，因为可能三个都是奇数圈平方，也有可能只有一个是奇数圈平方，另外两个是偶数圈平方
  • 那88个长度11的就更麻烦了

在代码上我选择先把那88个11解决掉，通过暴力枚举出所有阶为22（或阶为11）的回圈的组合o2Circles

然后再对那33个33（circles3）排列组合

然后再处理剩下简单的两种情况

参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
# sage
import hashlib
import itertools
from string import printable
from tqdm import tqdm

P2 = [41, 124, 256, 27, 201, 93, 40, 133, 47, 10, 69, 253, 13, 245, 165, 166, 118, 230, 197, 249, 115, 18, 71, 24, 100, 14, 160, 28, 251, 96, 106, 5, 244, 58, 67, 44, 150, 42, 255, 74, 168, 182, 153, 209, 227, 232, 159, 128, 125, 11, 135, 90, 76, 30, 84, 31, 1, 149, 48, 95, 216, 94, 157, 131, 196, 172, 105, 169, 202, 203, 121, 210, 53, 9, 147, 89, 39, 68, 59, 141, 87, 207, 51, 180, 19, 81, 57, 103, 228, 77, 12, 129, 185, 85, 45, 123, 50, 116, 65, 213, 104, 64, 54, 155, 222, 112, 3, 252, 21, 33, 138, 151, 211, 233, 204, 97, 239, 113, 82, 200, 23, 231, 177, 26, 72, 4, 78, 183, 199, 6, 49, 29, 250, 119, 32, 56, 110, 187, 35, 143, 83, 25, 70, 2, 66, 101, 217, 120, 224, 142, 191, 136, 189, 127, 132, 36, 174, 146, 152, 140, 193, 62, 178, 17, 148, 248, 167, 88, 73, 229, 134, 156, 158, 60, 63, 242, 221, 34, 214, 20, 171, 139, 226, 186, 164, 181, 236, 107, 111, 61, 99, 108, 179, 223, 137, 212, 237, 102, 161, 145, 184, 173, 247, 162, 205, 154, 55, 117, 254, 38, 75, 234, 7, 46, 109, 22, 175, 144, 219, 220, 195, 190, 98, 79, 15, 170, 80, 235, 52, 8, 37, 243, 198, 86, 43, 192, 241, 240, 208, 130, 188, 114, 218, 215, 206, 176, 238, 16, 246, 126, 122, 163, 225, 92, 91, 194]
c = [18, 188, 48, 47, 100, 234, 225, 8, 187, 34, 124, 113, 118, 252, 137, 196, 125, 20, 251, 168, 167, 5, 225, 134, 66, 203, 26, 148, 63, 181, 213, 124, 170, 234, 35, 120, 47, 69, 157, 69, 194]

P2G = PermutationGroupElement(P2)
print(P2G)
#exit(0)
'''
(1,41,168,88,103,54,30,96,123,177,221,195,137,110,33,244,215,109,21,115,204,162,62,94,85,19,197,237,241,188,107,3,256,194,223,98,116,97,50,11,69,202,173,158,146,101,104,155,132,29,251,122,231,37,150,142,25,100,213,7,40,74,9,47,159,152,136,56,31,106,112,151,191,99,65,196,212,234,86,81,87,57)
(2,124,26,14,245,206,154,127,78,68,169,73,53,76,89,228,235,43,153,189,111,138,187,236,192,108,252,163,178,34,58,149,224,79,59,48,128,183,226,170,229,52,90,77,39,255,91,12,253,225,15,165,148,120,200,145,66,172,156,36,44,209,254,92,129,199,161,193,179,214,46,232,243,218,144)
(4,27,160,140,143,70,203,247,238,240,130,6,93,185,164,17,118,113,211,75,147,217,175,63,157,174,60,95,45,227,80,141,83,51,135,32,5,201,184,186,181,171,134,119,82,207,55,84,180,20,249,246,176,242,114,233,198,102,64,131,49,125,72,210,38,42,182,139,35,67,105,222,190,61,216,22,18,230,8,133,250,126)
(16,166,248)
(23,71,121)
(117,239,208)
# and:
(10)(13)(24)(28)(167)(205)(219)(220)
'''

s = [10, 13, 24, 28, 167, 205, 219, 220]
o2Circles = set()
o2Circles.add('')
for si in tqdm(itertools.permutations(s)):
  tmp = []
  for i in range(0, len(si), 2):
    for t in tmp:
      if si[i] in t or si[i+1] in t:
        break
    else:
      tmp += [tuple(sorted([si[i], si[i+1]]))]
      o2Circles.add(''.join(str(x) for x in sorted(tmp)))
# print(list(o2Circles)[-1])  # random if no sorted...
o2Circles = sorted(list(o2Circles))
print(len(o2Circles))

def sqrtOdd(oddCircles):
  Ptmp = ''
  for oc in oddCircles:
    k = len(oc)
    assert k % 2 == 1
    k = (k - 1) // 2
    tmp = []
    for i in range(k):
      tmp += [oc[i]]
      tmp += [oc[k+i+1]]
    tmp += [oc[k]]
    Ptmp += str(tuple(tmp))
  return Ptmp
  
def sqrtEven(evenCircles):
  Ptmp = []
  if evenCircles == []:
    return []
  assert len(evenCircles) == 2
  assert len(evenCircles[0]) == len(evenCircles[1])
  k = len(evenCircles[0])
  if k % 2 == 1:
    Ptmp += [sqrtOdd([evenCircles[0]]) + sqrtOdd([evenCircles[1]])]
  for i in range(k):
    tmp = []
    for j in range(k):
      tmp += [evenCircles[0][j]]
      tmp += [evenCircles[1][(i+j)%k]]
    Ptmp += [str(tuple(tmp))]
  return Ptmp

circles3 = [
  (16,166,248),
  (23,71,121),
  (117,239,208)
]
evenCircles0 = [
  (1,41,168,88,103,54,30,96,123,177,221,195,137,110,33,244,215,109,21,115,204,162,62,94,85,19,197,237,241,188,107,3,256,194,223,98,116,97,50,11,69,202,173,158,146,101,104,155,132,29,251,122,231,37,150,142,25,100,213,7,40,74,9,47,159,152,136,56,31,106,112,151,191,99,65,196,212,234,86,81,87,57),
  (4,27,160,140,143,70,203,247,238,240,130,6,93,185,164,17,118,113,211,75,147,217,175,63,157,174,60,95,45,227,80,141,83,51,135,32,5,201,184,186,181,171,134,119,82,207,55,84,180,20,249,246,176,242,114,233,198,102,64,131,49,125,72,210,38,42,182,139,35,67,105,222,190,61,216,22,18,230,8,133,250,126)
]
oddCircles0 = [
  (2,124,26,14,245,206,154,127,78,68,169,73,53,76,89,228,235,43,153,189,111,138,187,236,192,108,252,163,178,34,58,149,224,79,59,48,128,183,226,170,229,52,90,77,39,255,91,12,253,225,15,165,148,120,200,145,66,172,156,36,44,209,254,92,129,199,161,193,179,214,46,232,243,218,144),
]

P0 = sqrtOdd(oddCircles0) 
for o2i in tqdm(o2Circles):           # 413/764 [24:42<20:59
#for o2i in tqdm(o2Circles[::-1]):    # 350/764 [19:43<23:20
  for ec0 in sqrtEven(evenCircles0):
    P1 = P0 + ec0
    for c3 in itertools.permutations(circles3):
      evenCircles1 = [c3[0], c3[1]]
      oddCircles1 = [c3[2]]
      P2 = P1 + sqrtOdd(oddCircles1) 
      for ec1 in sqrtEven(evenCircles1):
        P3 = P2 + ec1
        P4 = P3 + o2i
        PG = PermutationGroupElement(P4) 
        assert PG^2 == P2G

        P = list(PG.dict().values())
        Ph = hashlib.sha512(str(P).encode()).digest()
        flag = ''.join([chr(x^^y) for x, y in zip(Ph, c)])
        if 'brics' in flag or 'BRICS' in flag:
          print(P)
          print(flag)
          exit(0)

'''
[190, 226, 217, 195, 155, 62, 20, 96, 176, 24, 227, 169, 220, 52, 76, 248, 197, 54, 17, 40, 238, 103, 239, 10, 55, 229, 137, 28, 186, 8, 64, 104, 143, 193, 81, 187, 119, 196, 127, 249, 61, 212, 145, 236, 11, 79, 242, 218, 151, 45, 146, 245, 15, 230, 100, 102, 222, 179, 243, 97, 168, 93, 223, 106, 38, 189, 87, 12, 80, 215, 208, 99, 225, 246, 107, 165, 154, 91, 232, 202, 67, 142, 158, 213, 164, 35, 105, 22, 148, 206, 68, 252, 94, 185, 50, 133, 95, 174, 210, 84, 32, 31, 18, 5, 57, 131, 147, 92, 247, 140, 156, 49, 241, 152, 240, 60, 23, 237, 150, 235, 117, 171, 250, 170, 191, 221, 255, 144, 163, 162, 112, 184, 123, 37, 101, 198, 160, 36, 86, 33, 173, 207, 244, 183, 153, 135, 3, 228, 214, 82, 125, 233, 66, 39, 201, 138, 98, 51, 114, 110, 34, 6, 199, 19, 89, 16, 205, 216, 253, 26, 231, 111, 83, 116, 194, 47, 126, 161, 149, 7, 122, 234, 2, 29, 85, 251, 44, 75, 172, 41, 72, 254, 58, 63, 27, 42, 118, 56, 178, 43, 132, 141, 109, 130, 167, 77, 25, 121, 192, 65, 188, 182, 180, 224, 203, 88, 256, 128, 219, 13, 4, 1, 157, 46, 53, 124, 69, 120, 14, 30, 134, 59, 136, 139, 200, 209, 113, 115, 71, 204, 211, 159, 48, 70, 90, 9, 21, 166, 74, 177, 181, 129, 73, 108, 78, 175]
brics+{ab99943f6dae4f20595c8645fcf8289e}

 54%|██████████████████████████████████                             | 413/764 [24:42<20:59,  3.59s/it]
'''

PS：这只是针对输入的代码，通解的代码好像有点麻烦，就先留坑了

PPS：set()会有个坑，就是每次输出的顺序都是不一样的，导致复现的时候时间不准，后面加了sorted测出顺序爆破24:42，逆序19:43，完整爆破40min+，可以考虑多线程了（阴间题

参考·

  • Judson T W. Abstract algebra: theory and applications[M]. 2020.
  • https://math.stackexchange.com/questions/266569/how-to-find-the-square-root-of-a-permutation