（ 原文地址：https://0xffff.one/d/1046-sage-sheng-cheng-chao-chao-chao-da-su-shu/2 ）

前言·

前段时间在CINTA群讨论MSP(Modular Subset Product problem)的时候搞了个这样的程序，然后被@“Bintou”#55 问到“next_prime输入很大时跑半天都跑不出来”，试了一下，除了next_prime，random_prime也是这样。于是水了篇帖子。。。

正文·

这里我选择直接看Sage里next_prime和random_prime的代码是怎么实现的，先找random_prime的，介绍一个很chun但很实用的定位代码位置的方法：python报错的时候会显示报错代码的位置，所以随便输点会让random_prime报错的输入就好，比如字符串。

然后找到random_prime的实现大概如下：

1
2
3
4
5
6
7
8
9
10
11
12
def random_prime(n, proof=None, lbound=2):
    ... ...
    if proof:
        prime_test = is_prime
    else:
        prime_test = is_pseudoprime
    randint = ZZ.random_element
    while True:
        # In order to ... ....
        p = randint(lbound, n)
        if prime_test(p):
            return p

就是随机选一个lbound到n的数做素性测试，通过则返回，不通过则选另一个。这里注意到一个叫proof的参数，当proof是False的时候做的是伪素数(Pseudoprime)的测试（至于怎么测的和伪到什么程度，先留个坑…），伪素数的测试比素数的测试(指is_prime)快很多，所以做random_prime时，把第二个参数设成False，速度大大提升，问题解决，但生成的是伪素数。

next_prime同，第二个参数设False，生成伪素数，速度提升（next_prime的做法好像是先找下一个伪素数，然后再判断是不是真素数的，设False的话就不做真素数的判断，有兴趣可以自己看源码）

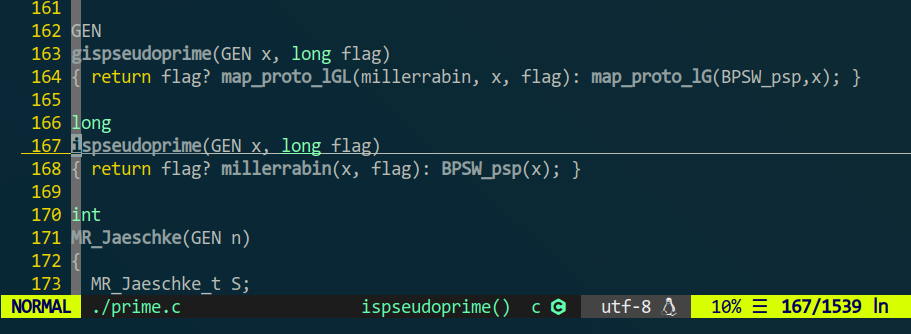
另外，Sage的is_pseudoprime()用的是pari的ispseudoprime()，翻了一下… …/pari-2.13.2/src/basemath/prime.c，167行写的就是调用Miller-Rabin（或BPSW_psp？）：

总结·

加个False